地衡風
天気図上に見られる高気圧や低気圧のようなスケールの現象では, 大気に働く力として, コリオリ力と気圧傾度力の2つの力が支配的になる.
この2つの力が働いている場合の空気塊の東西\((x)\)方向および南北\((y)\)方向の運動方程式は次式で書くことができる.
\[\frac{du}{dt} = fv -\frac{1}{\rho}\frac{\partial p}{\partial x} \]
\[\frac{dv}{dt} = -fu -\frac{1}{\rho}\frac{\partial p}{\partial y}\]
風速の時間変化が小さく, 左辺の時間変化項が右辺の他の項に比べて無視できると仮定すれば, 次式となる.
\[u = -\frac{1}{f} \cdot \frac{1}{\rho}\frac{\partial p}{\partial y} \]
\[v = \frac{1}{f} \cdot \frac{1}{\rho}\frac{\partial p}{\partial x} \]
このように, コリオリ力と気圧傾度力の2力のつり合いによって求まる風\((u, v)\)を地衡風という.
図に地衡風の概念図を示す. 北半球では, 地衡風は高気圧を右に見ながら等圧線に平行に吹く. これは, 高気圧から低気圧に向かう気圧傾度力とコリオリ力がつり合った結果である.
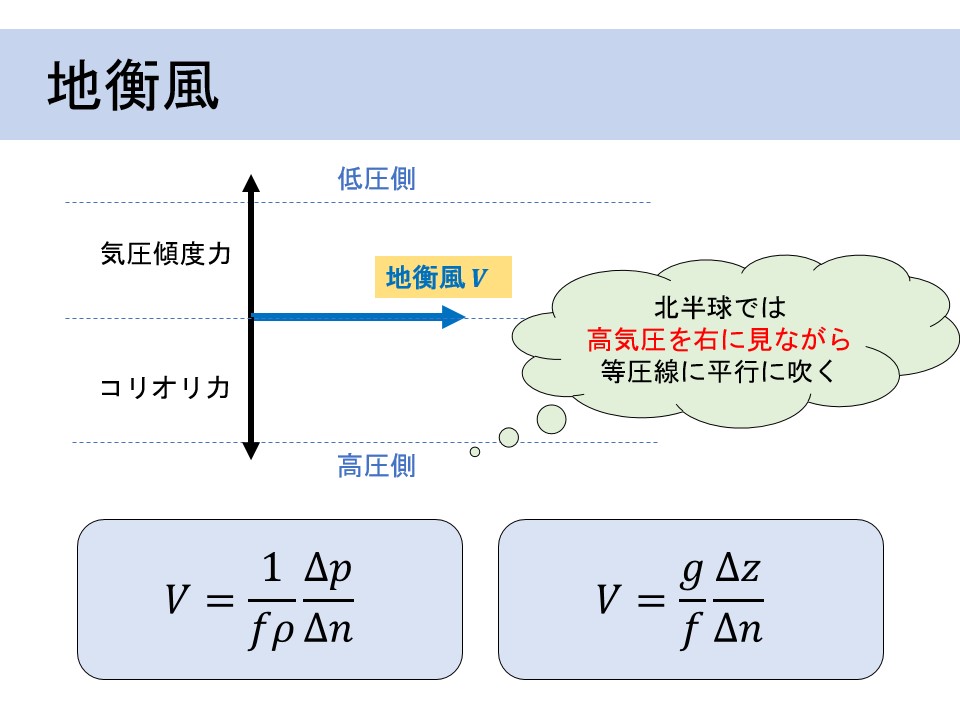
ここまでの議論では地衡風を\(x, y\)の各成分に分けて考えてきたが, 天気図から風速を推定する場合には, 一般に次のような方法を用いる.
まず, コリオリ力と気圧傾度力のつり合い式の微分を差分化し, 風速ベクトルの各成分を2乗して足し合わせ, 両辺のルートを取ると, 次式が得られる.
\[\sqrt{u^2+v^2} = \frac{1}{f\rho}\cdot\frac{\Delta p}{\frac{\Delta x\Delta y}{\sqrt{(\Delta x)^2+(\Delta y)^2}}} \]
図に示すように気圧勾配の向きを\(n\)軸とすれば, 右辺の分母は次式である.
\[\Delta n= \frac{\Delta x\Delta y}{\sqrt{(\Delta x)^2+(\Delta y)^2}} \]
地衡風の風速\(V_\sigma(=\sqrt{u^2+v^2})\)は, 次式となる.
\[V_\sigma = \frac{1}{f\rho}\cdot\frac{\Delta p}{\Delta n} \]
一般的に天気図では\(4\mathrm{\,hPa}\)ごとに等圧線が引かれているので, 2つの等圧線の間隔がわかれば, 上式を使っておおよその風速を推定することができる.


