傾度風
前々節では気圧傾度力とコリオリ力のつり合いとして地衡風を考えたが, 日々の天気図を見ていても等圧線が直線であることは稀で, 多かれ少なかれ曲がっている. 例えば, 低気圧や高気圧の中心付近では等圧線が閉じた曲線になっているのが普通である.
地衡風の考えに基づけばこのことは, 低気圧や高気圧周りの空気塊は曲がりながら運動していることを意味する.
したがって等圧線の曲率の大きな所では遠心力が無視できなくなる. 遠心力は風速の2乗に比例し曲率半径に反比例するため, 台風の中心付近のように風速が大きく曲率半径の小さいところでは, 特にこの遠心力の効果が重要になる.
気圧傾度力とコリオリ力(転向力)に遠心力を加えた3力のつり合いを傾度風平衡という. そしてその結果として生じる風を傾度風という. 図(傾度風)に傾度風平衡の状態と傾度風との関係を示す.
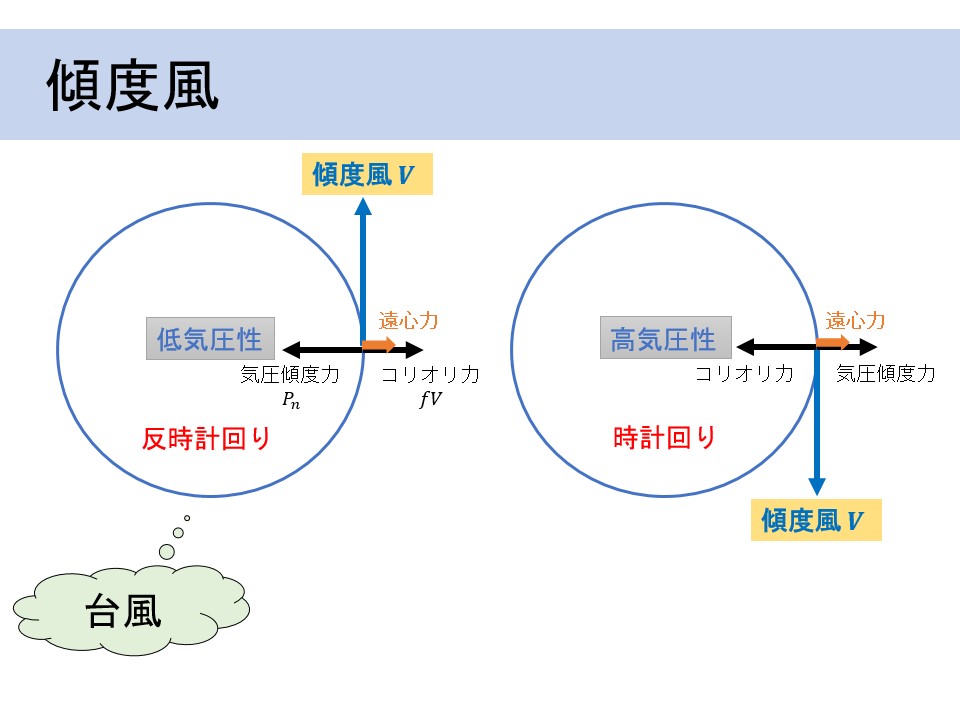
低気圧性の流れでは, 地衡風平衡と同様, 低気圧中心向きに気圧傾度力, 外向きにコリオリ力(転向力)が働いている. 傾度風平衡ではこれに外向きの遠心力が加わって, 反時計周りの傾度風が生じる.
地衡風と比べると, 遠心力が加わって外向きのコリオリ力(転向力)が小さくて済む分, 風速は傾度風の方が小さくなる.
次に高気圧性の流れを見ると, 外向きの気圧傾度力と遠心力に対して, 内向きのコリオリ力(転向力)がつり合い, 時計周りの傾度風が生じる.
地衡風平衡に比べて, 遠心力が外向きに働く分だけコリオリ力は大きくなるため, 傾度風の風速は地衡風よりも大きくなる.
次にこの傾度風平衡を数式で表すことを考えてみる.
同心円状の高気圧・低気圧の半径\(r\)のところを速度\(V\)で回る空気塊に働く力のつり合いは, 次式となる.
\[\frac{V^2}{r} + fV = P_n\]
ここで, \(f\)はコリオリ係数, \(P_n\)は気圧傾度力である.
低気圧の場合は\(V>0,\,P_n>0\), 高気圧の場合は\(V<0,\,P_n<0\)と考えればよい.
3力のつり合い式1は\(V\)に関する2次方程式となっており, その解は次式である.
\[V = \frac{1}{2}(-hr\pm \sqrt{(fr)^2+4rP_n})\]
ここで解は2つ出てくるが, 半径\(r\)が大きくなるほど\(V\)は地衡風に近づくという条件から, 通常括弧内の符号は正号である.
3力のつり合い式2からは低気圧と高気圧に関して興味深い違いが浮かび上がってくる. \(V\)が実数となるためにはルート内が\(0\)以上でなければならないという条件があるため, 高気圧(\(P_n<0\))の場合, 次式が満たされなければならない.
\[-P_n < \frac{f^2r}{4}\]
つまり, 高気圧性の流れでは半径\(r\)が小さいところでは気圧傾度\(P_n\)の大きさもそれに応じて小さくなければならない.
これに対して, 低気圧の場合では\(P_n>0\)なのでルート内は常に\(0\)以上となり, 気圧傾度に対する制約はなくなる.
こうして台風の風のように低気圧に伴っては強風が吹くのに対し, そのような強い気圧傾度や風を伴う高気圧は存在しないのである.


