Ⅲー1
Ⅲー2
Ⅲー3
Ⅲー4
Ⅲー5
Ⅲー6
Ⅲー7
Ⅲー8
Ⅲー9
Ⅲー10
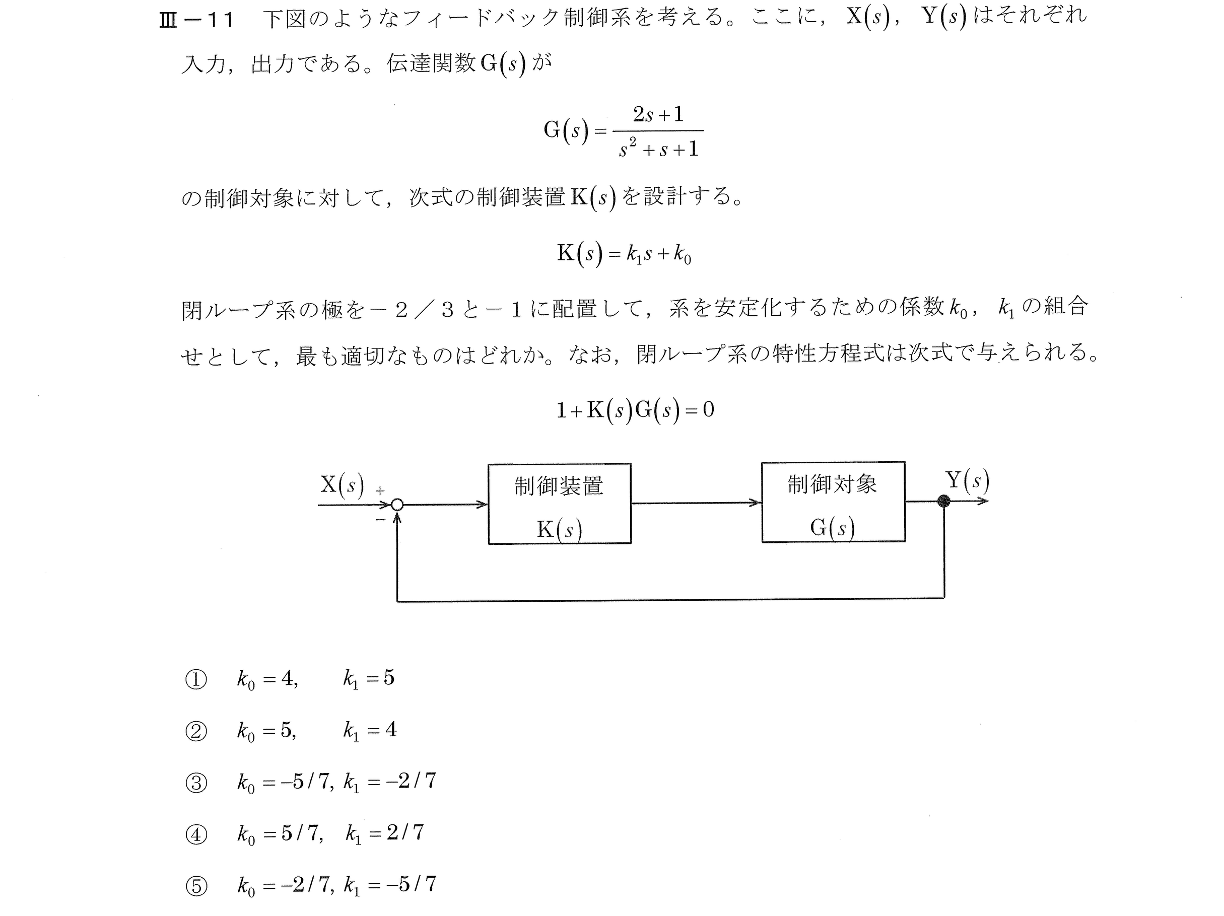
Ⅲー11
Ⅲー12

関数\(F(s)\)を逆ラプラス変換するために、部分分数分解を行う。
$$F(s) = \frac{1}{(s-3)(s+2)} = \frac{1}{5}\left(\frac{1}{s-3}-\frac{1}{s+2}\right) $$
したがって、原関数\(f(t)\)は、
$$f(t) = \frac{1}{5}(e^{3t}-e^{-2t})$$
【解答:⑤】
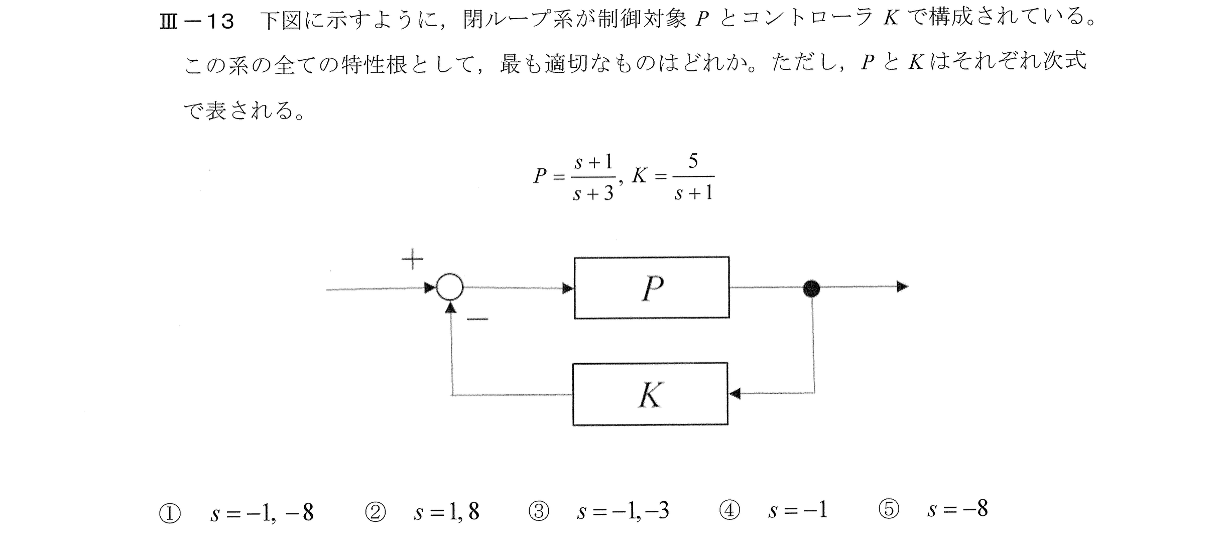
Ⅲー13
Ⅲー14
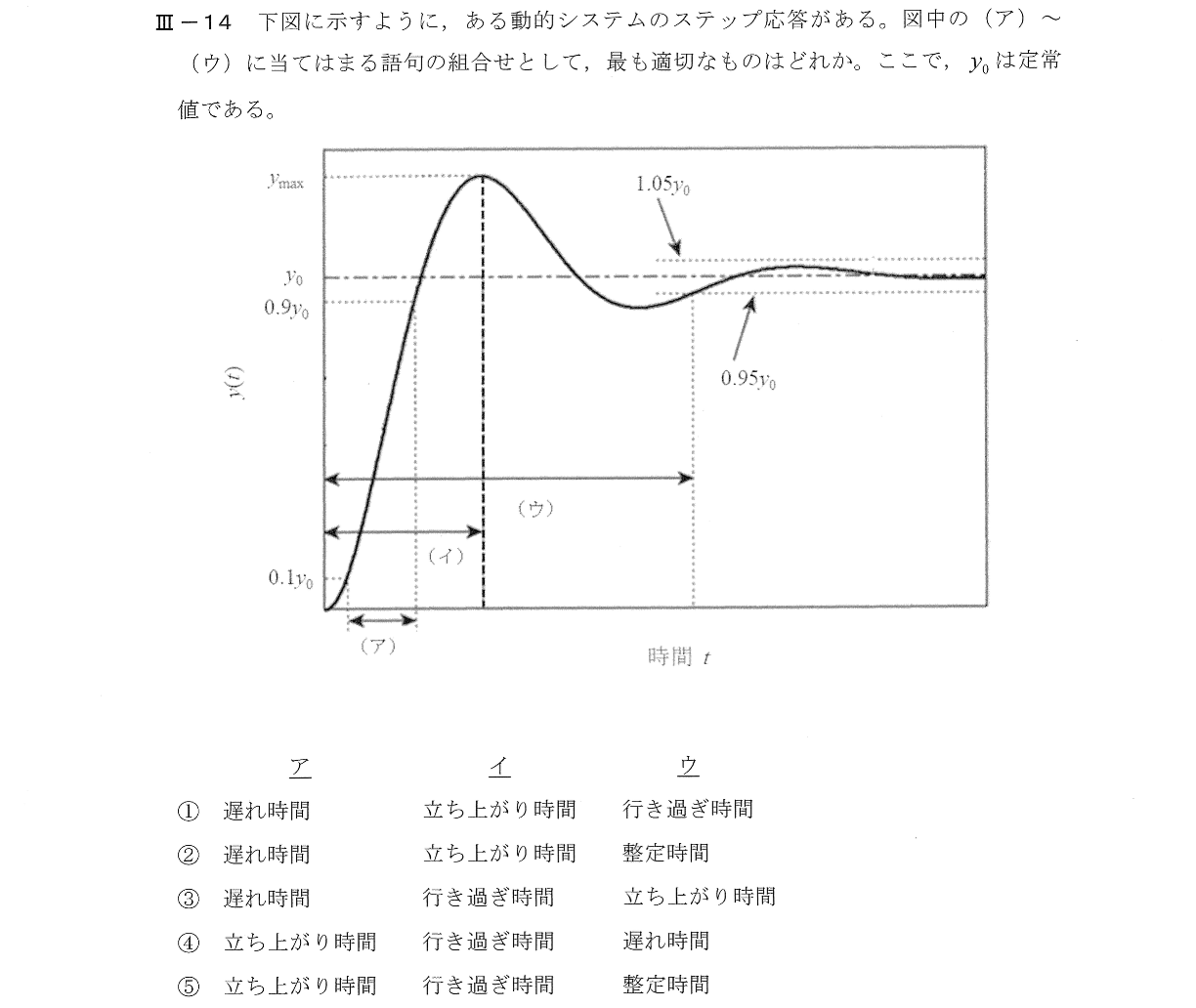
用語の定義を図と対応させて覚える。
【解答:⑤】
Ⅲー15

減衰比ではなく、減衰係数なら正。
【解答:⑤】
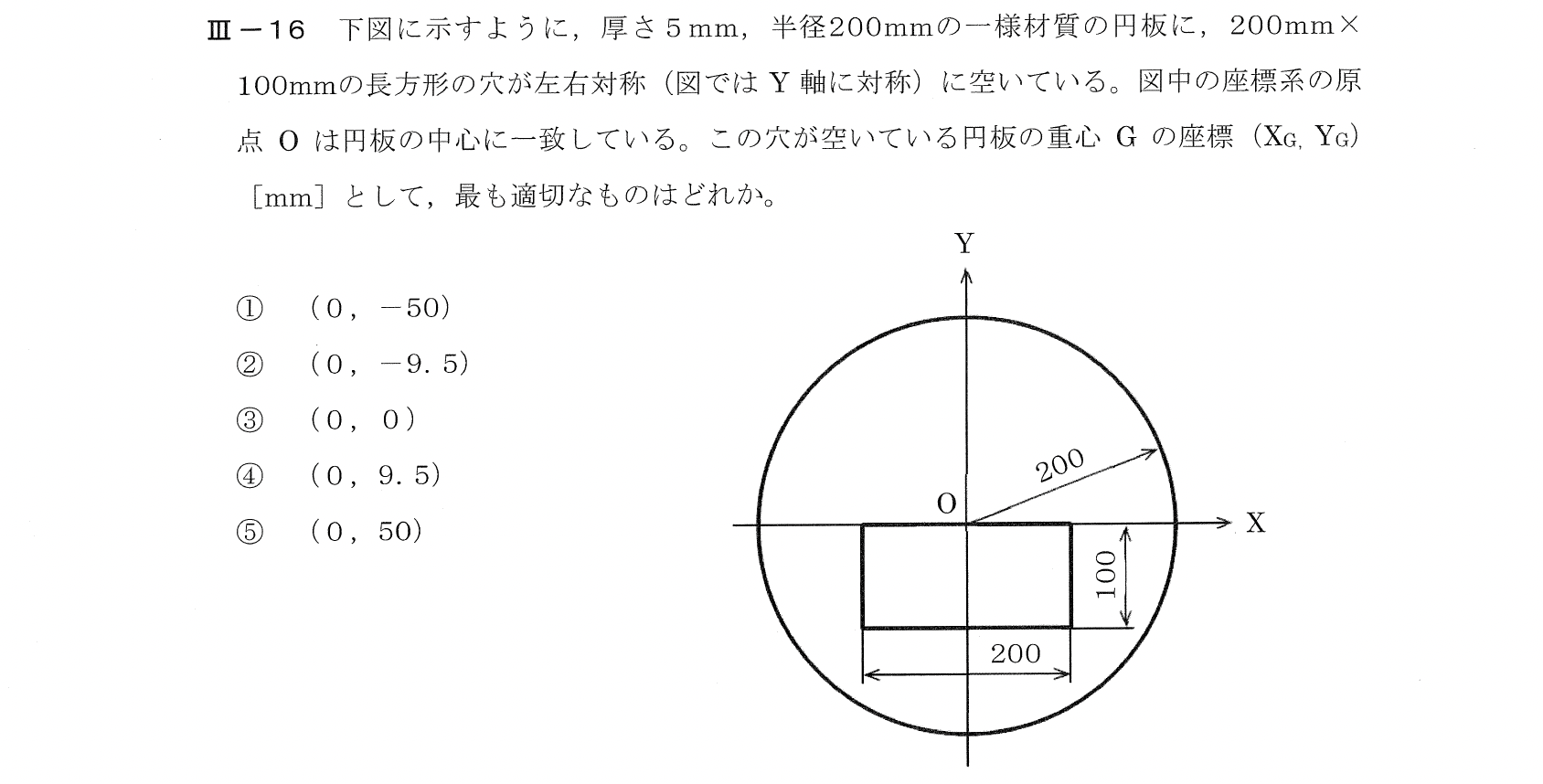
Ⅲー16
Ⅲー17
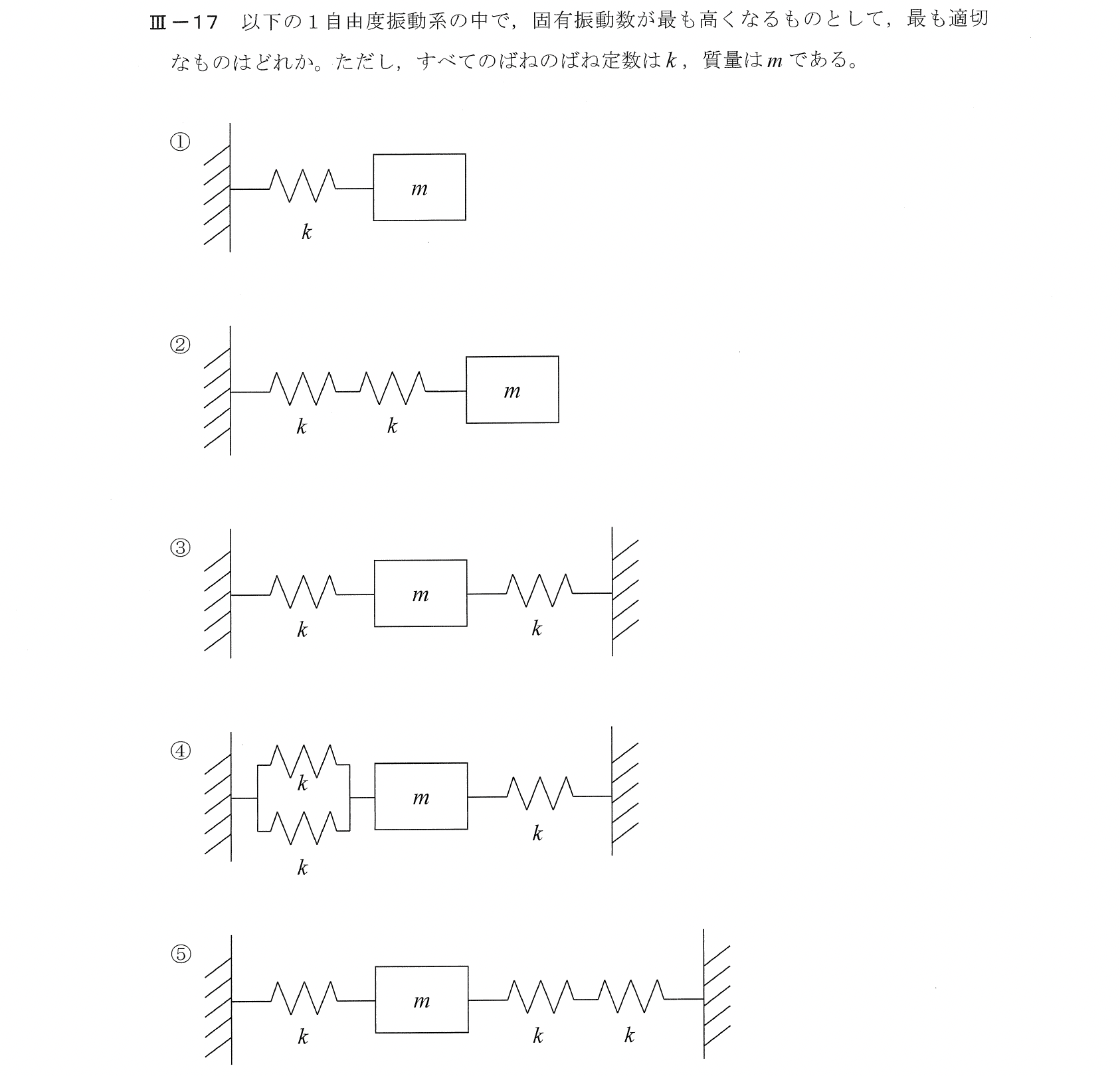
合成ばね定数を考えて、固有角振動数を求める。
$$1. \omega_n=\sqrt{\frac{k}{m}}$$
$$2. \omega_n=\sqrt{\frac{k/2}{m}}$$
$$3. \omega_n=\sqrt{\frac{2k}{m}}$$
$$4. \omega_n=\sqrt{\frac{3k}{m}}$$
$$5. \omega_n=\sqrt{\frac{3k/2}{m}}$$
【解答:④】
Ⅲー18
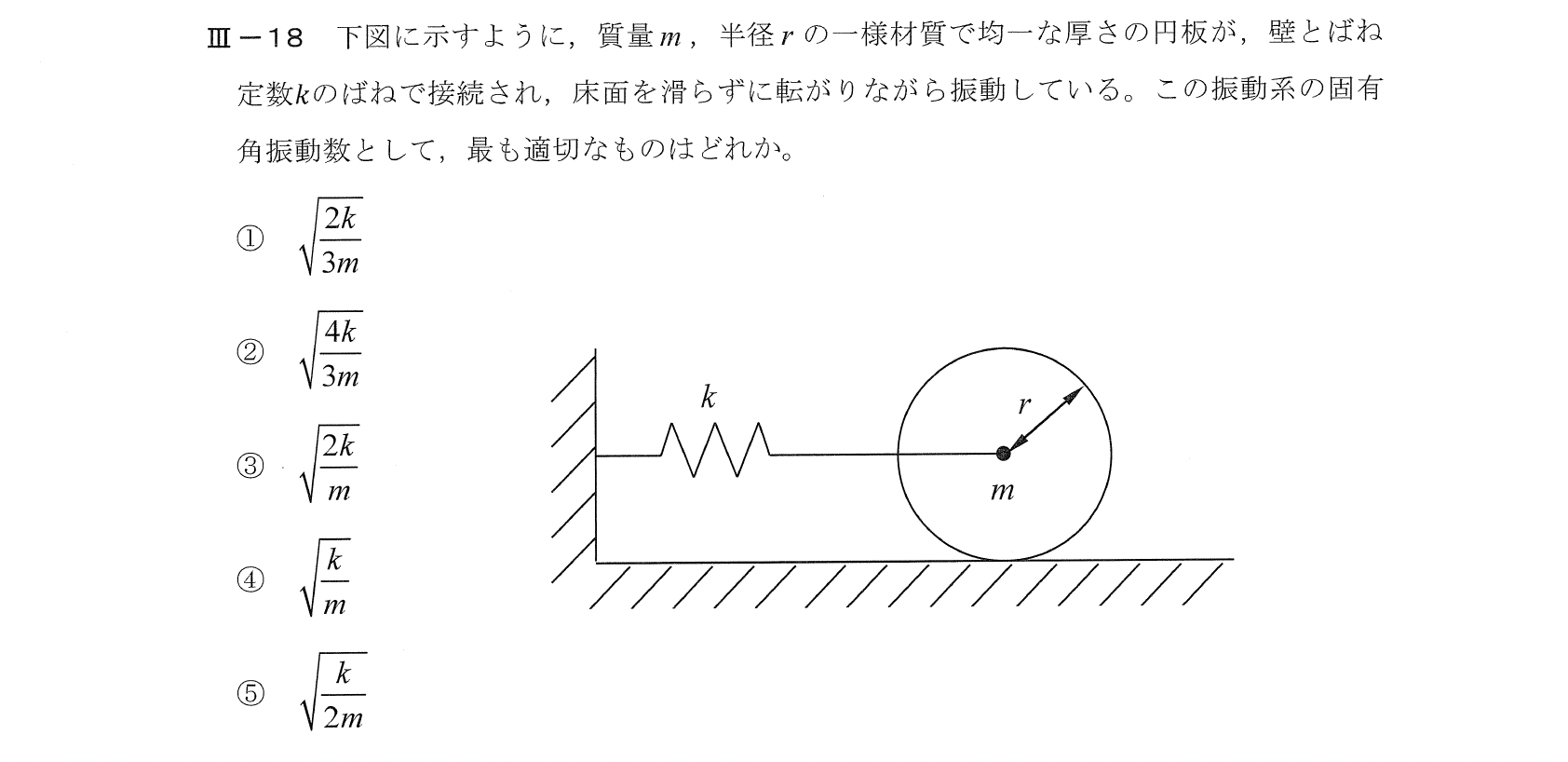
Ⅲー19

用語の定義を覚える。
【解答:②】
Ⅲー20
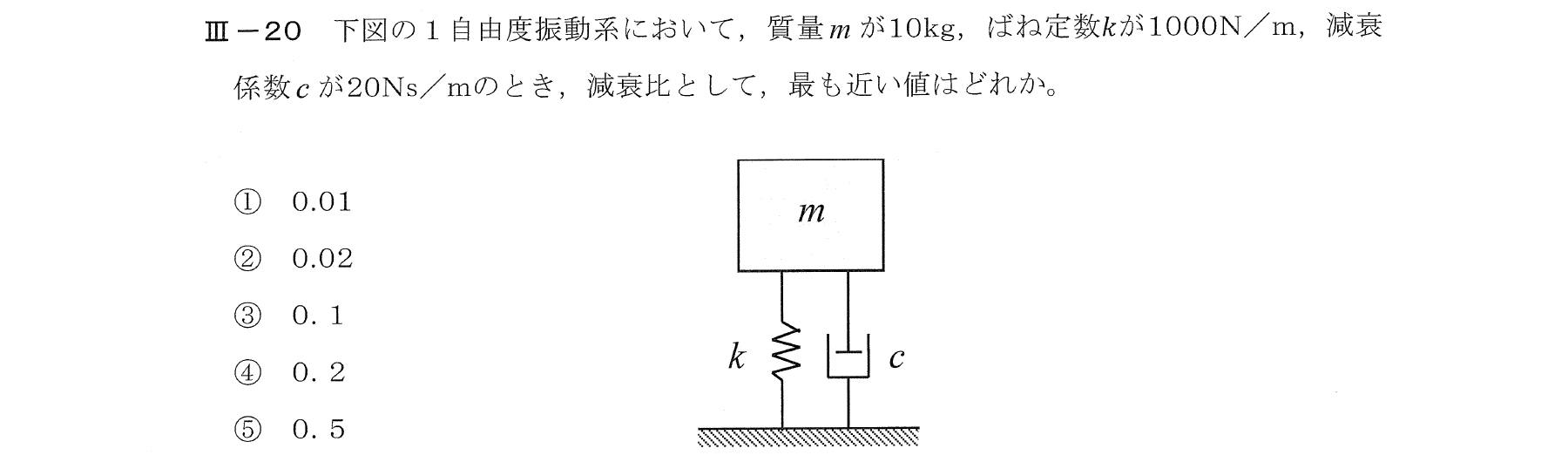
減衰比 \(\zeta\) は次式で表せる。
$$\zeta=\frac{c}{2\sqrt{mk}}$$
よって、\(c\) と \(m\) と \(k\) の値を代入する。
【解答:③】
Ⅲー21
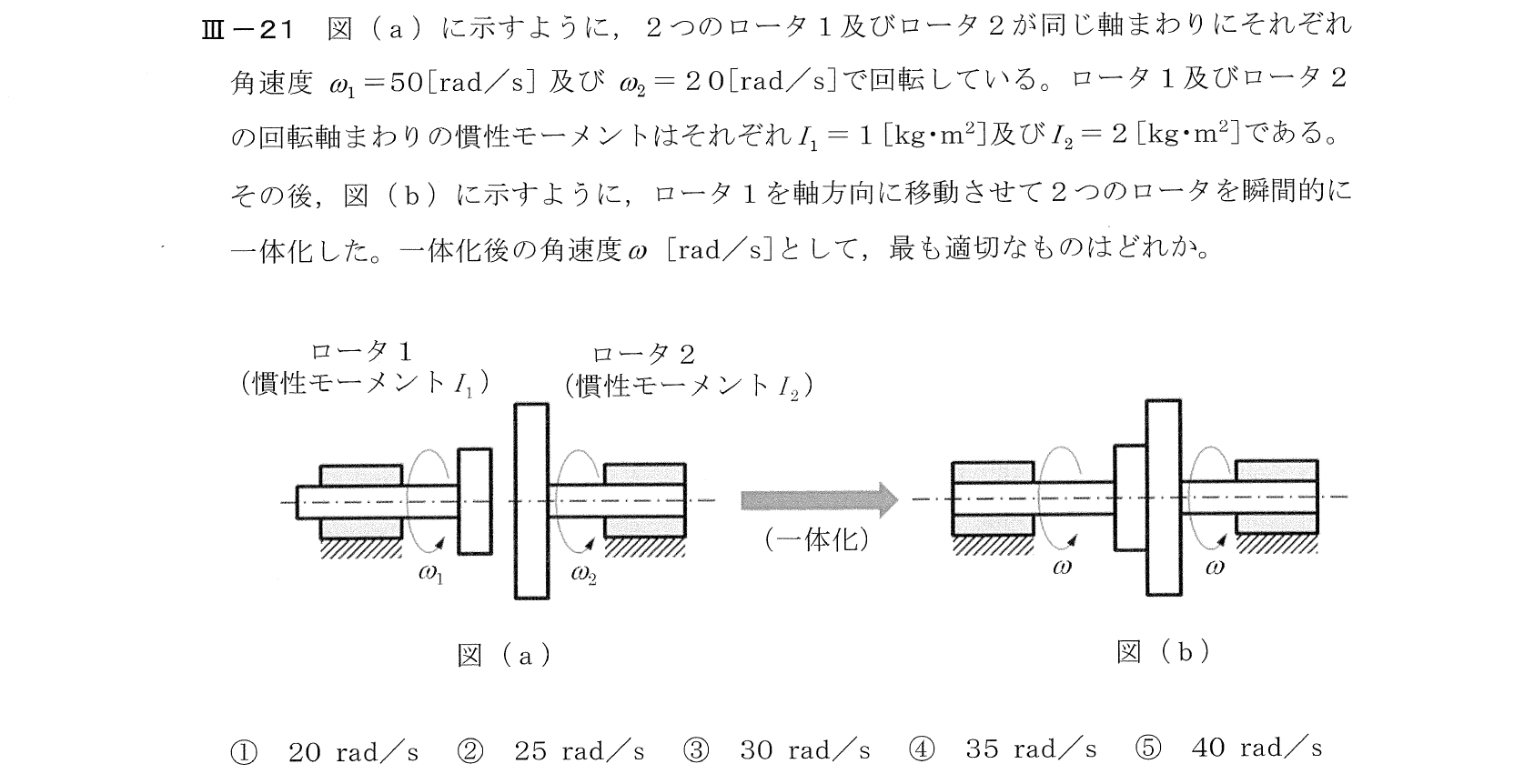
Ⅲー22

覚える。
【解答:①】
Ⅲー23

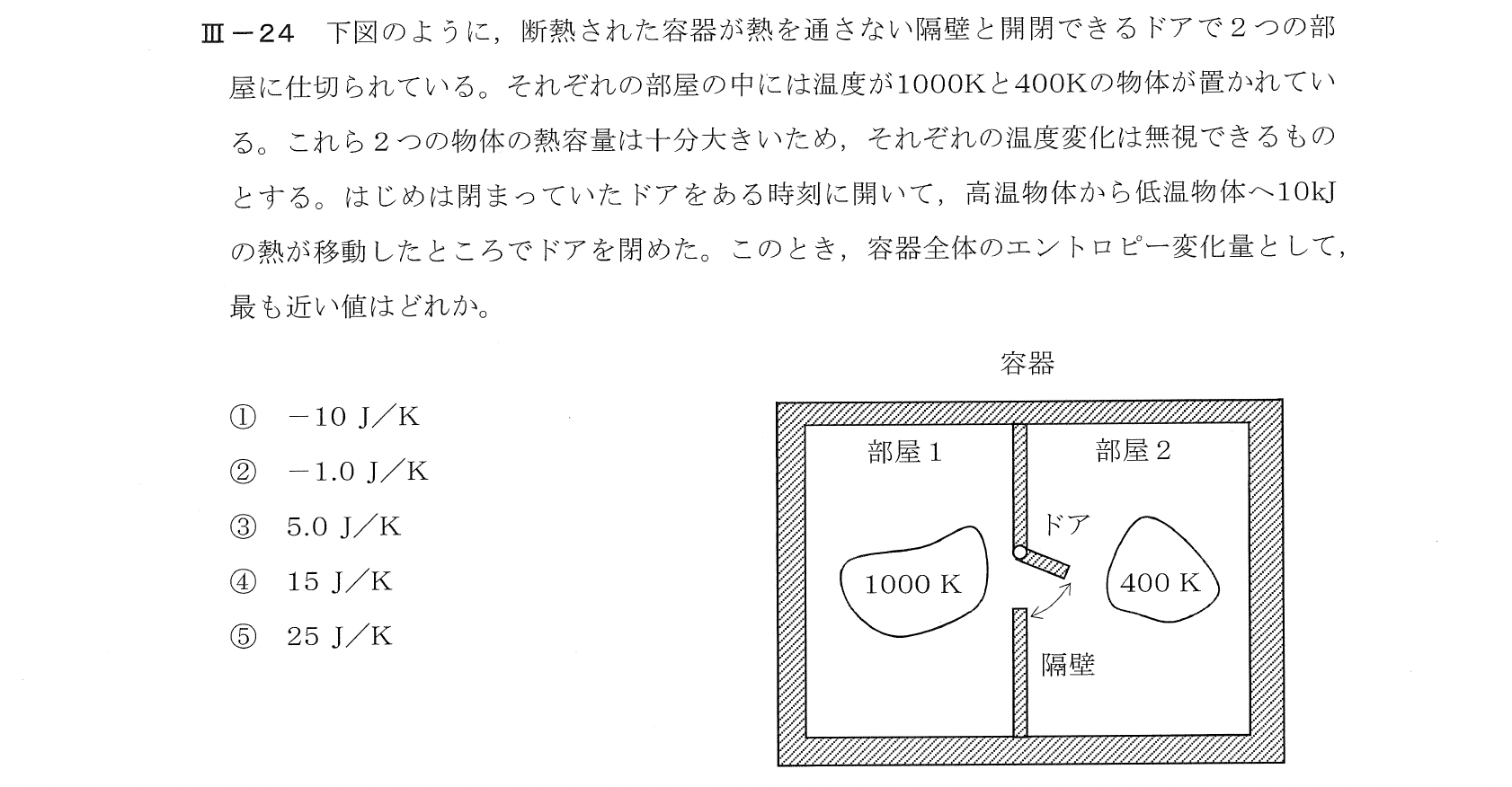
Ⅲー24
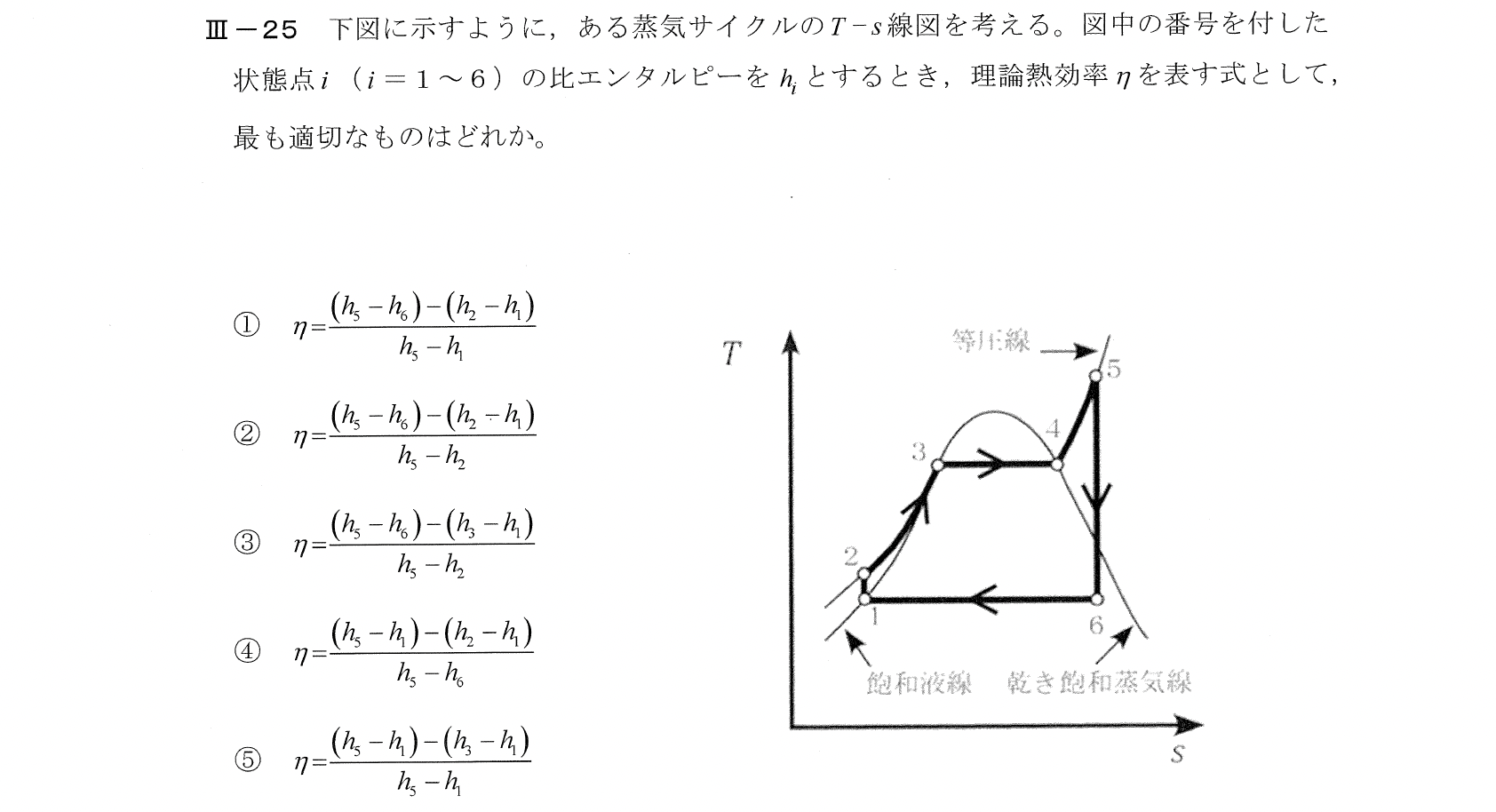
Ⅲー25
Ⅲー26

Ⅲー27

Ⅲー28

Ⅲー29

Ⅲー30

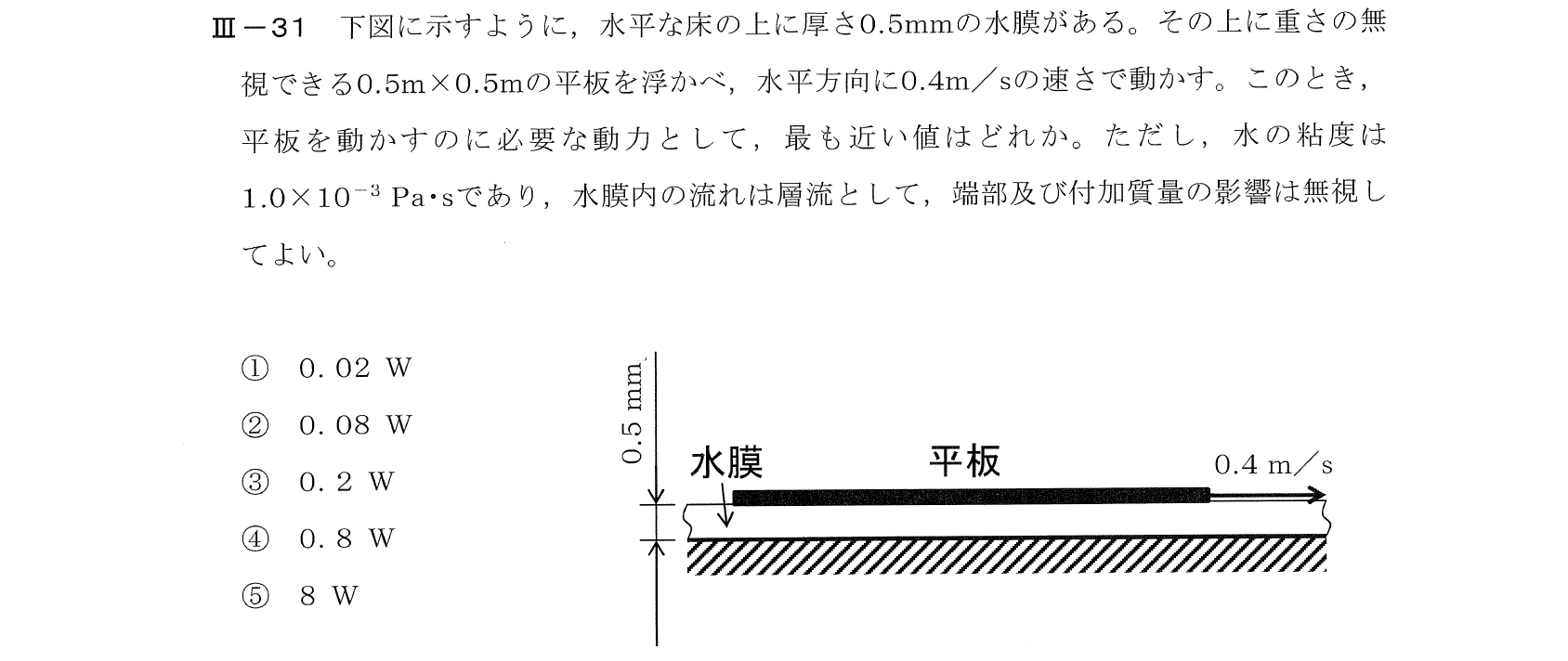
Ⅲー31
Ⅲー32

Ⅲー33

Ⅲー34

Ⅲー35


