Ⅲー1
Ⅲー2
Ⅲー3
Ⅲー4
Ⅲー5
Ⅲー6
Ⅲー7
Ⅲー8
Ⅲー9
Ⅲー10
Ⅲー11

Ⅲー12

関数\(F(s)\)を逆ラプラス変換するために、部分分数分解を行う。
$$F(s) = \frac{s+1}{(s+2)^2+1} = \frac{s+2}{(s+2)^2+1}-\frac{1}{(s+2)^2+1} $$
したがって、原関数\(f(t)\)は、
$$f(t) = e^{-2t}(\cos{t}-\sin{t})$$
【解答:①】
Ⅲー13

特性方程式は次式となる。
$$ s^2+5s+6 = (s+2)(s+3) = 0 $$
$$ s = -2, -3 $$
システムの安定性の条件は、すべての極の実部が負であることである。
今回求まった極 \(-2\) と \(-3\) はいずれも負の実数である。
したがって、この系は安定である。
【解答:②】
Ⅲー14
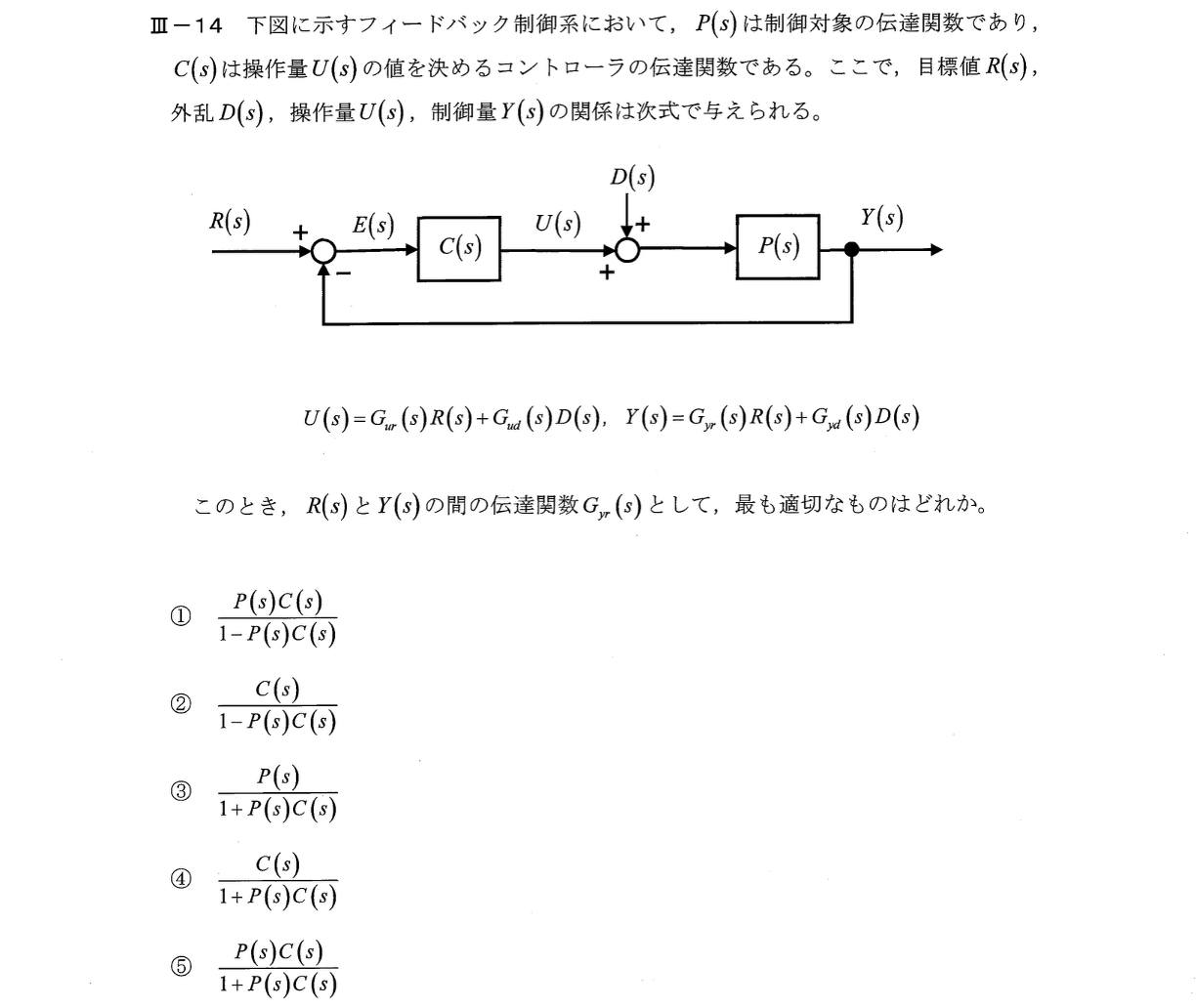
フィードバック結合の公式を用いる。
【解答:⑤】
Ⅲー15

ラグラジアン\(L=T-U\)を原点を支点として考える。
並進運動のエネルギーと回転運動のエネルギーを足し合わせた運動エネルギー\(T\)は次式となる。
$$T=\frac{1}{2}m{\dot{r}}^2+\frac{1}{2}mr^2{\dot{\theta}}^2$$
重力による位置エネルギーとばねの弾性エネルギーを足し合わせた位置エネルギー\(U\)は次式となる。
$$U=-mgr\cos{\theta}+\frac{1}{2}k(r-L)^2$$
【解答:④】
Ⅲー16

Ⅲー17
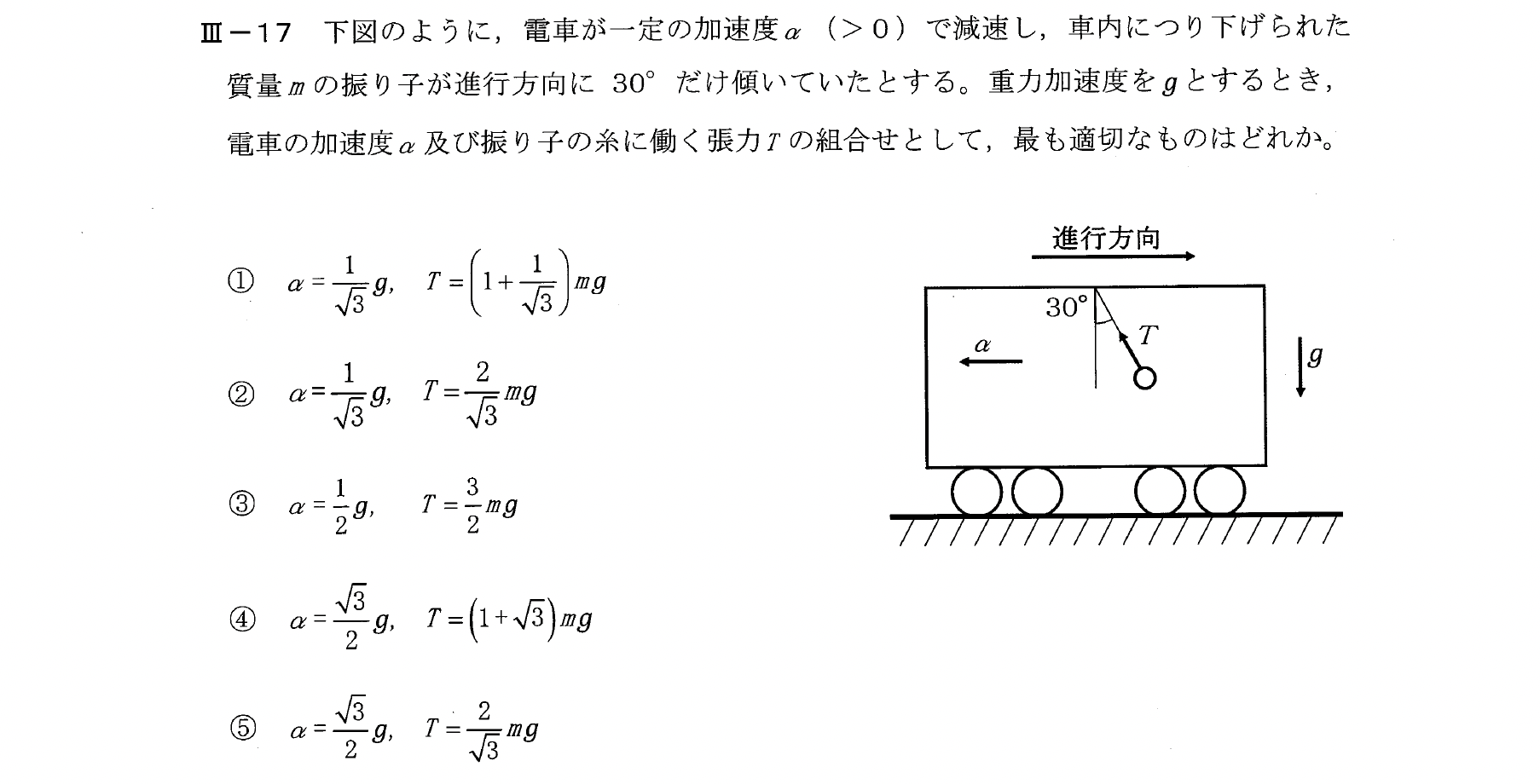
慣性系で力のつり合いを考える。
【解答:⑤】
Ⅲー18
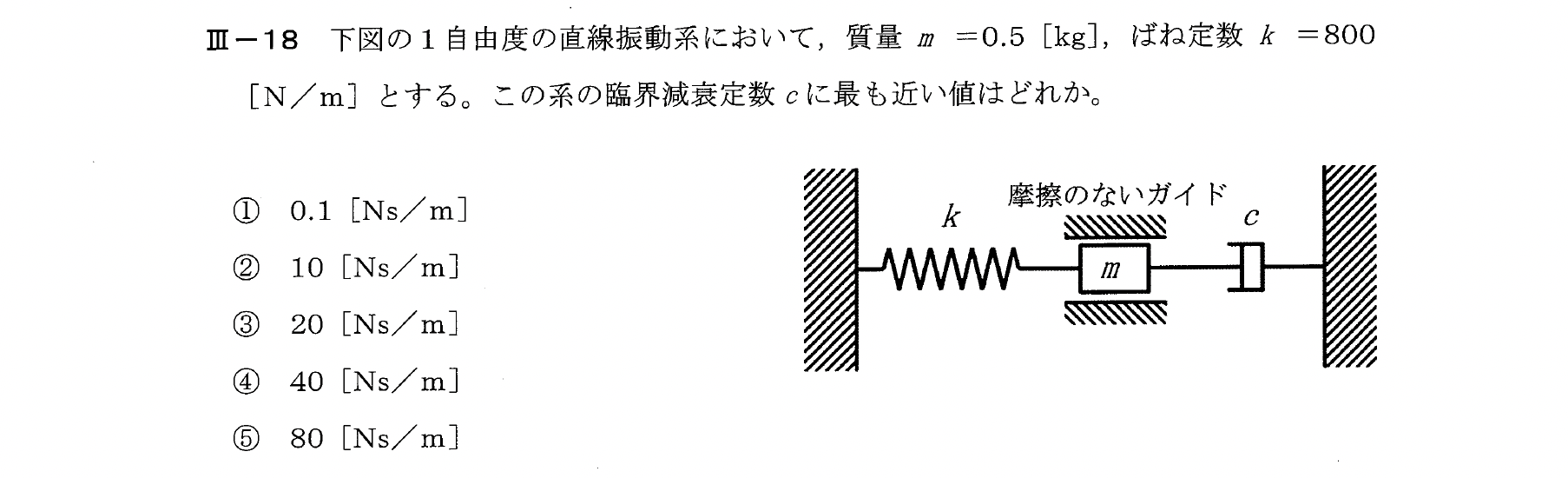
減衰比 \(\zeta\) は次式で表せる。
$$\zeta=\frac{c}{2\sqrt{mk}}$$
臨界減衰は、\(\zeta=1\)の場合である。
よって、\(c\) について式を整理して \(\zeta=1\) と \(m\) と \(k\) の値を代入する。
【解答:③】
Ⅲー19
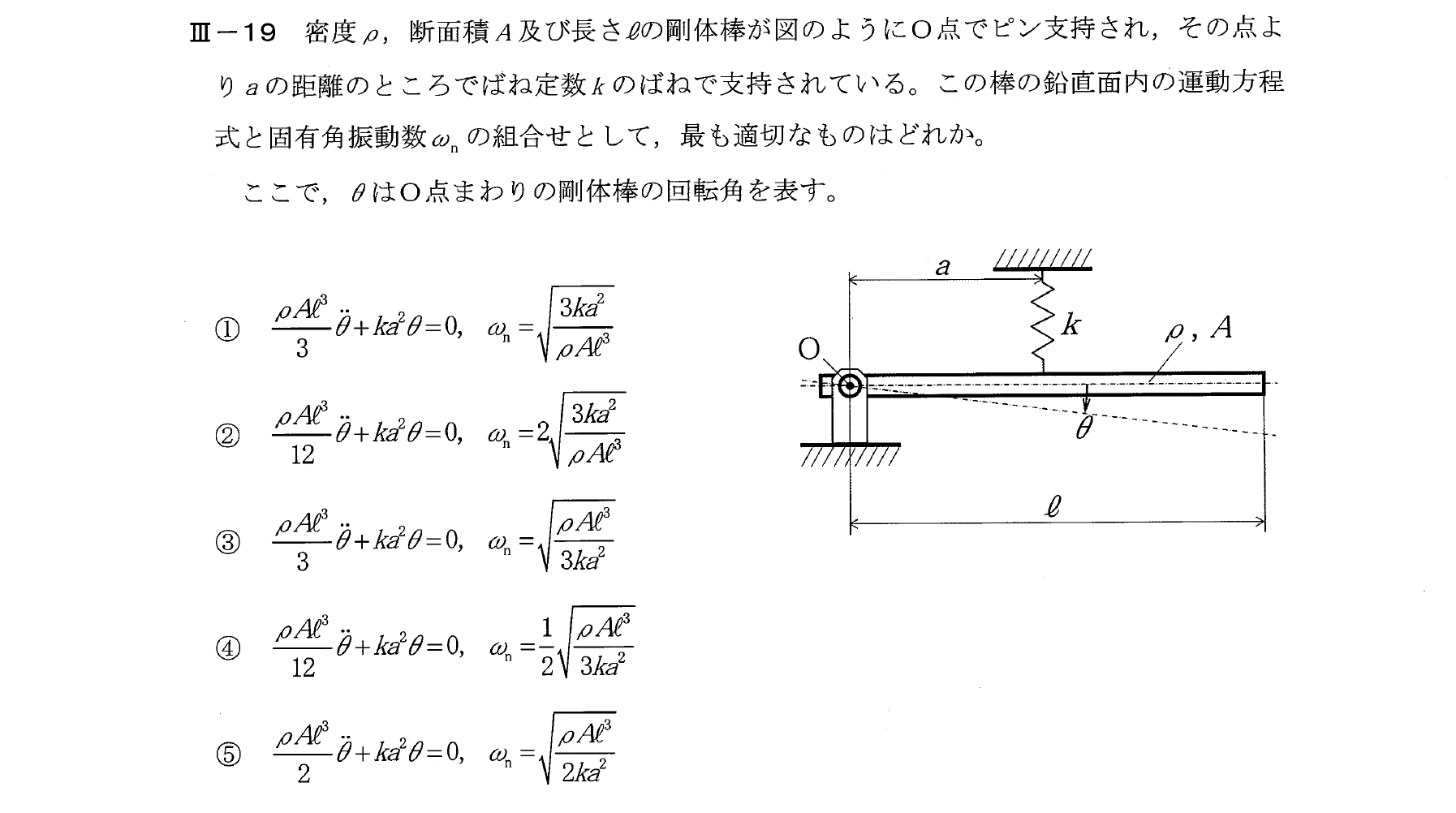
角運動方程式は次式となる。
$$I\ddot{\theta}+ka^2\theta=0$$
ここで、\(I\) はO点周りの慣性モーメントである。
\(I\) は平行軸の定理を用いると、一様棒の場合は次式となる。
$$I=I_G+\left(\frac{l}{2}\right)^2 m = \frac{ml^2}{12} + \frac{ml^2}{4} = \frac{ml^2}{3}$$
よって、回転運動の固有角振動数 \(\omega_{n}\) は次式となる。
$$\omega_{n}=\sqrt{{\frac{ka^2}{\frac{\rho Al^3}{3}}}}=\sqrt{{\frac{3ka^2}{\rho Al^3}}}$$
【解答:①】
Ⅲー20
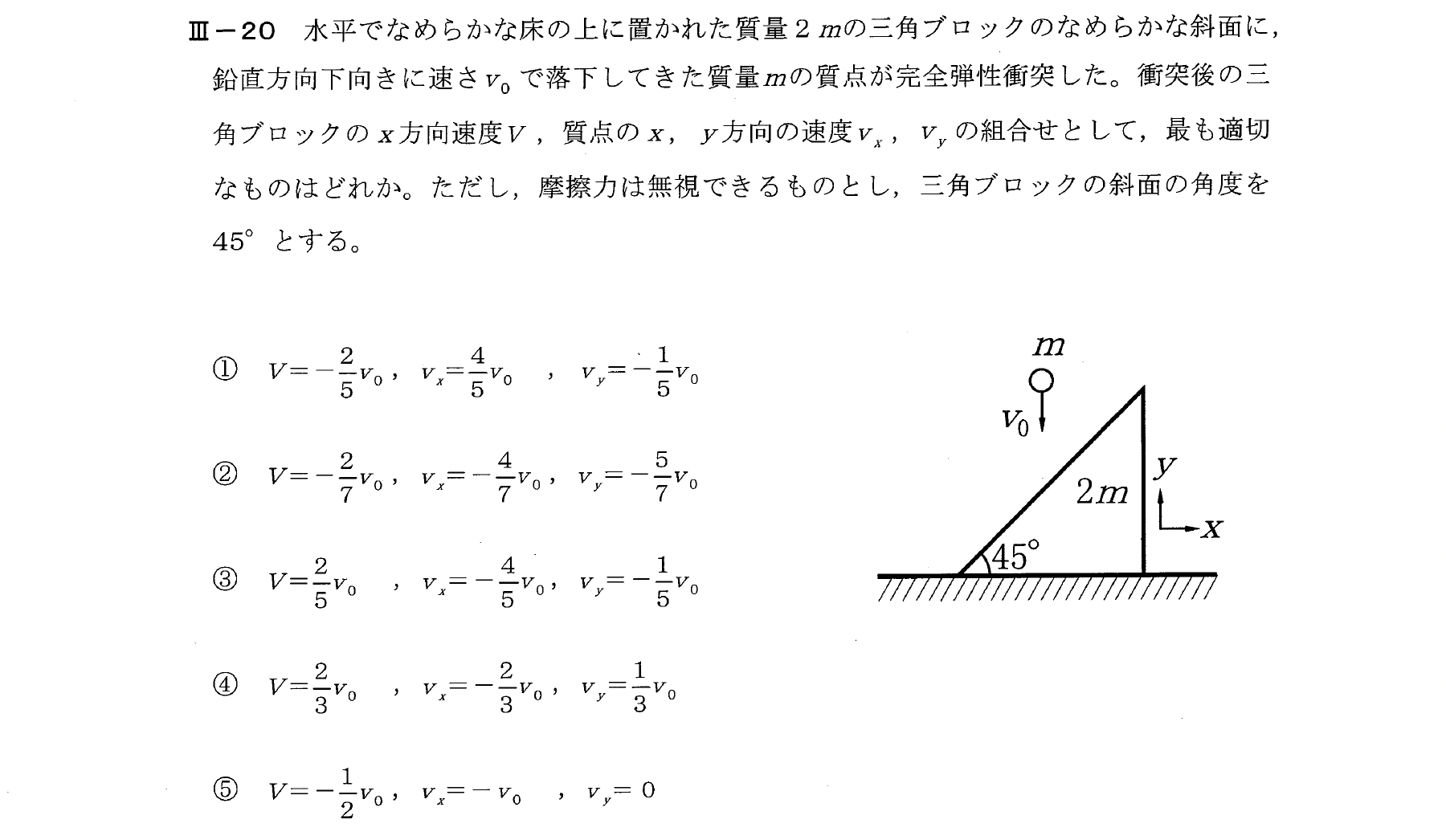
水平方向の運動量保存則を考える。
$$0=mv_x+2mV$$
$$v_x=-2mV$$
これを満たす選択肢は①か③しかない。
また、\(V\)が正であることは自明であるため反発係数の式を立式するまでもない。
【解答:③】
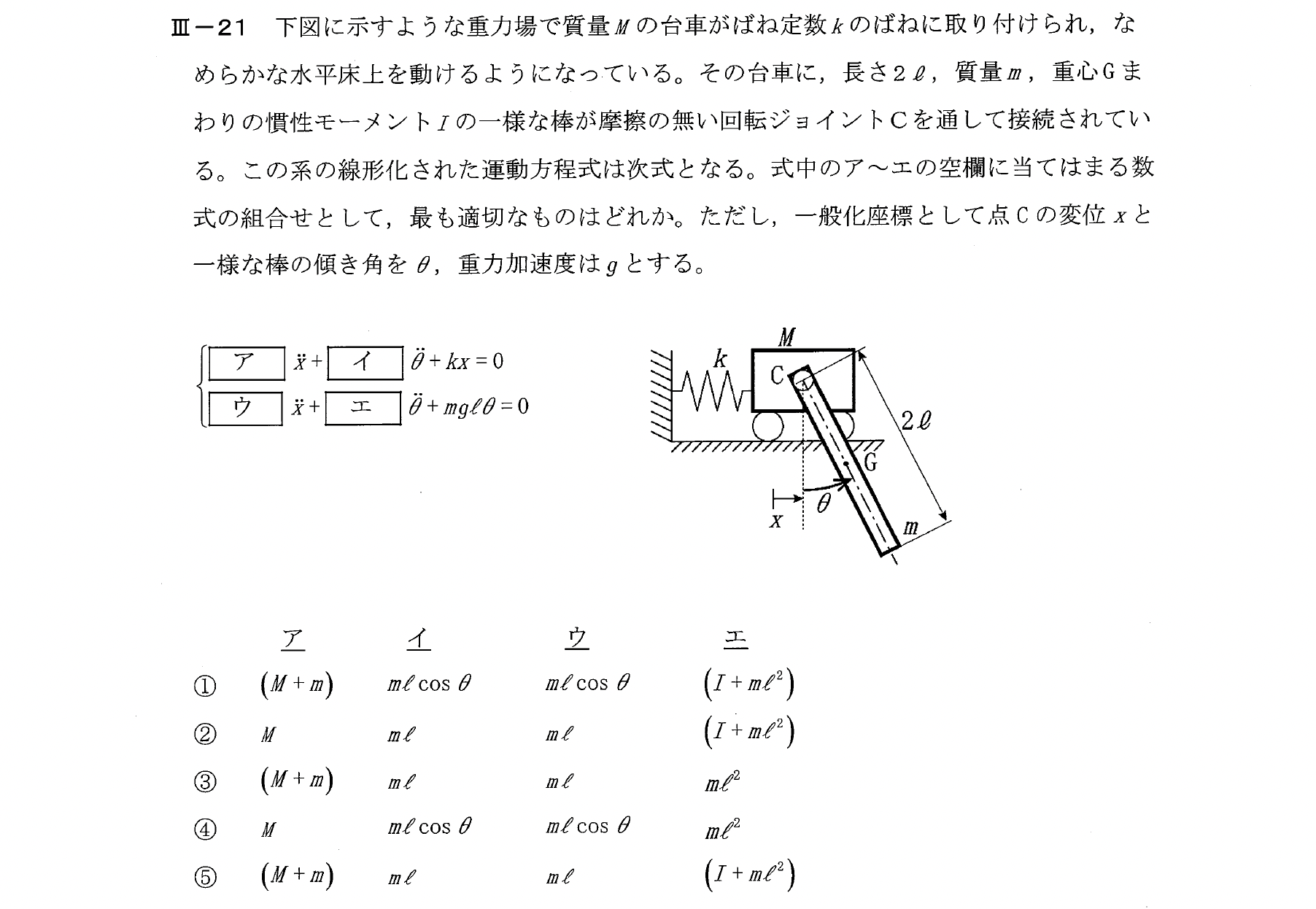
Ⅲー21
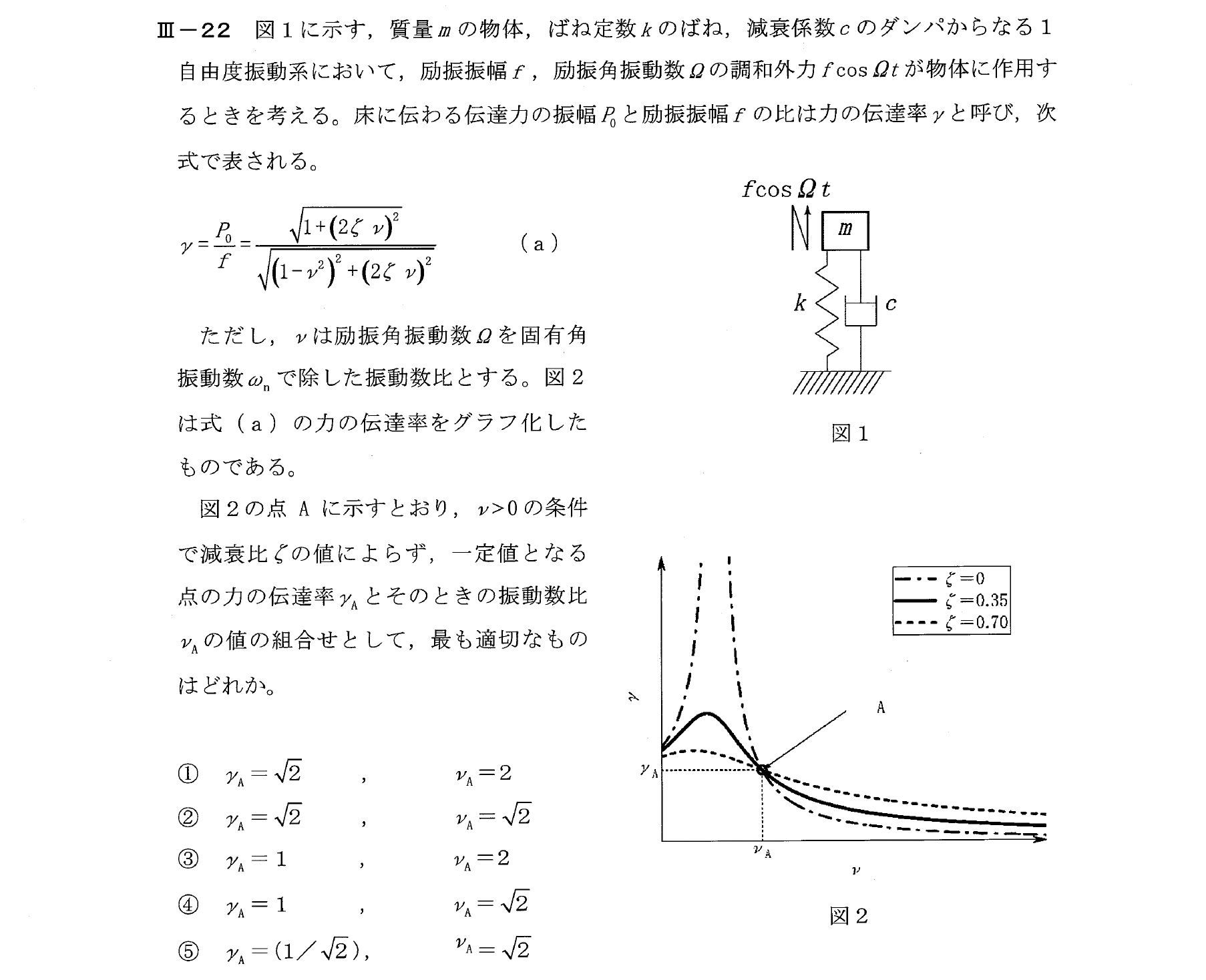
Ⅲー22
Ⅲー23
Ⅲー24
Ⅲー25
Ⅲー26
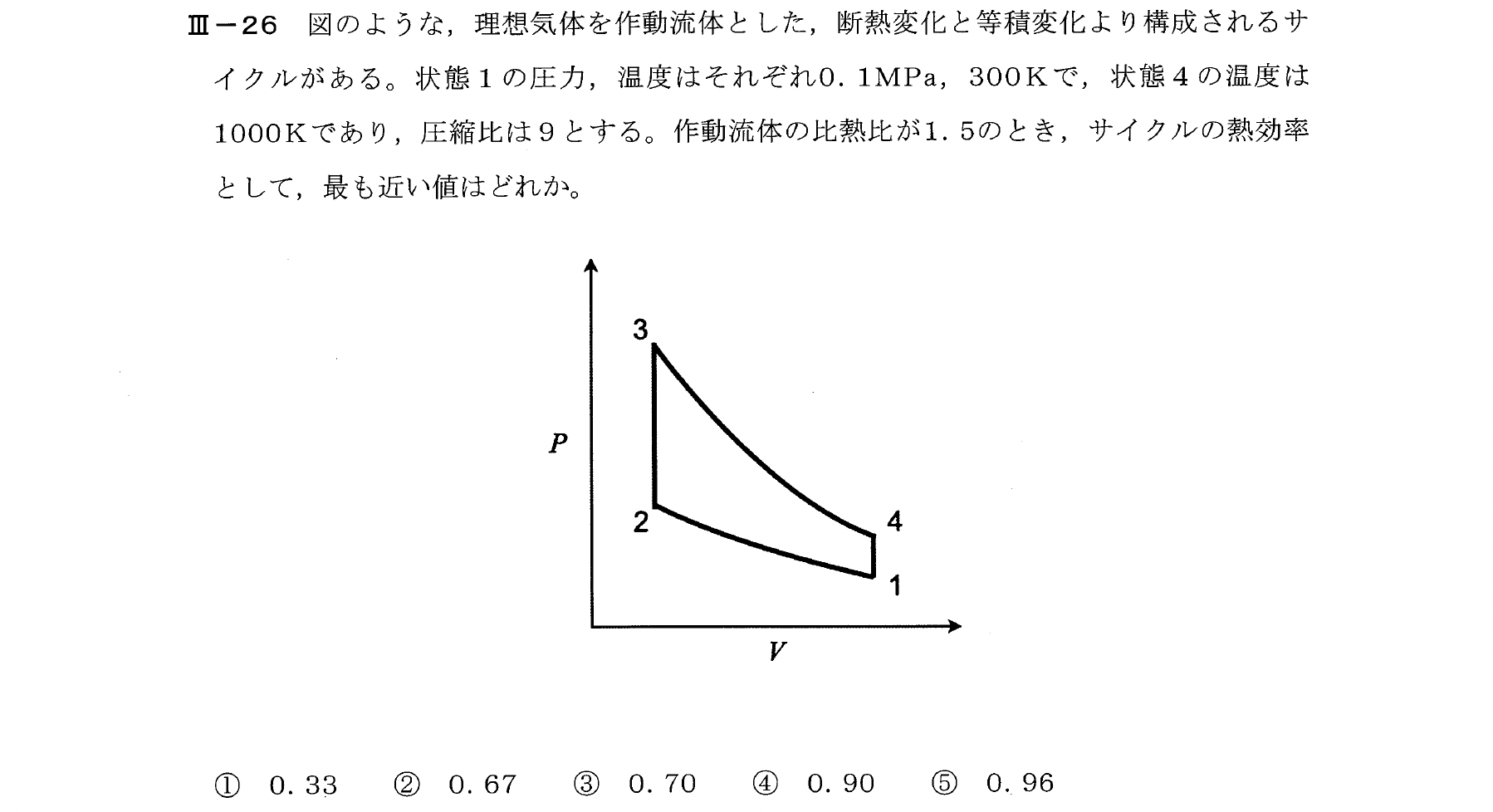
オットーサイクルの熱効率 \(\eta\) は次式で表せる。
$$\eta=1- \frac{1}{{\varepsilon}^{\kappa-1}}$$
圧縮比 \(\varepsilon=9\) と比熱比 \(\kappa=1.5\) の値を代入する。
【解答:②】
Ⅲー27
Ⅲー28
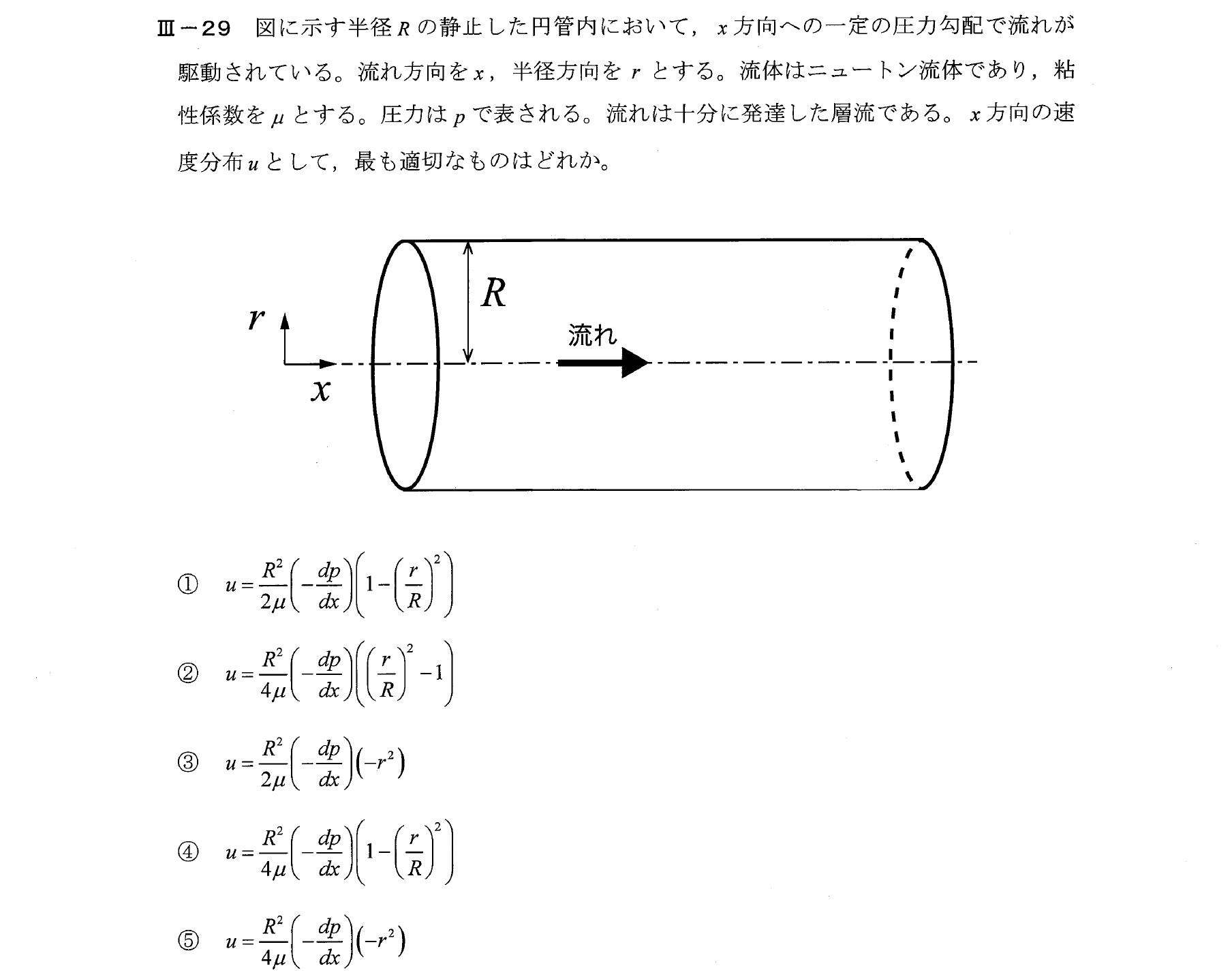
Ⅲー29
Ⅲー30

2次元の流れの場合、渦度は次式で求められる。
$$\omega=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$
【解答:③】
Ⅲー31
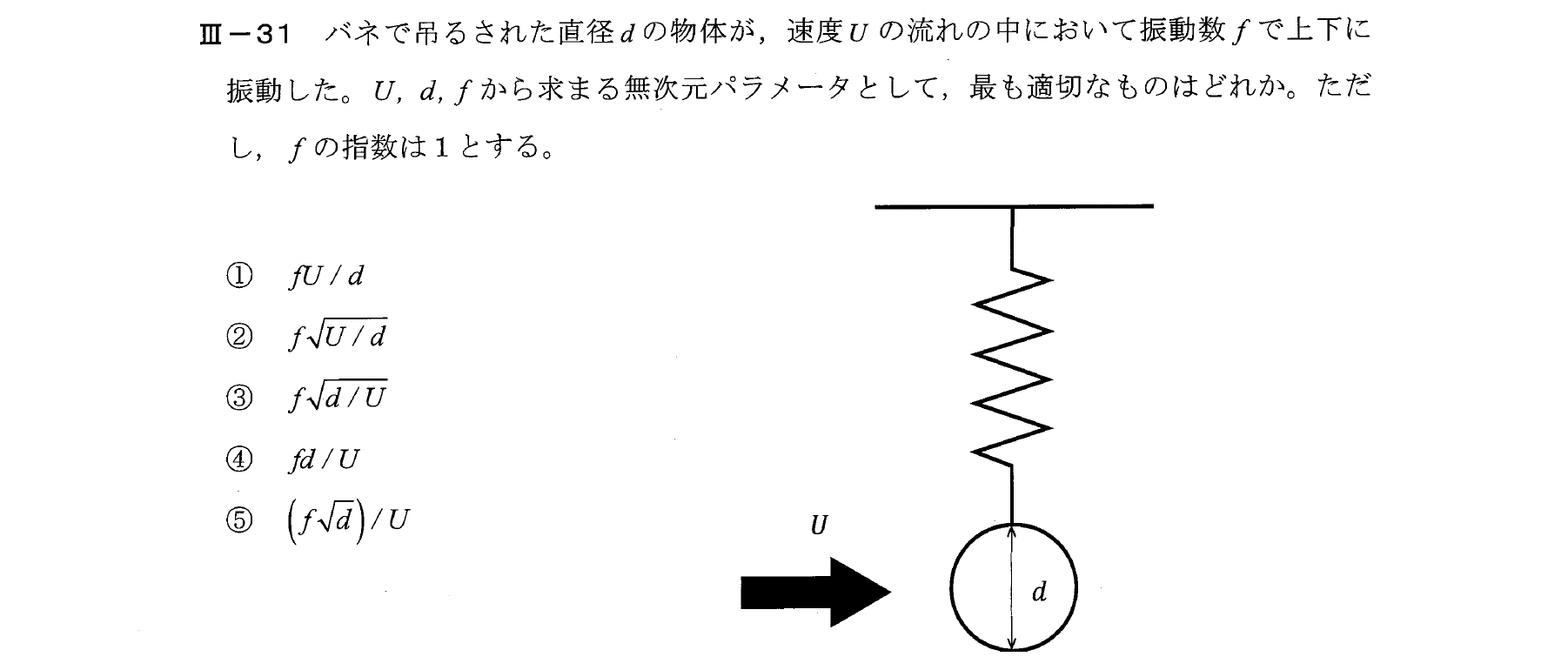
次元解析を行い、無次元量を作る。
$$d=[m]$$
$$U=[m/s]$$
$$f=[1/s]$$
【解答:④】
Ⅲー32

Ⅲー33
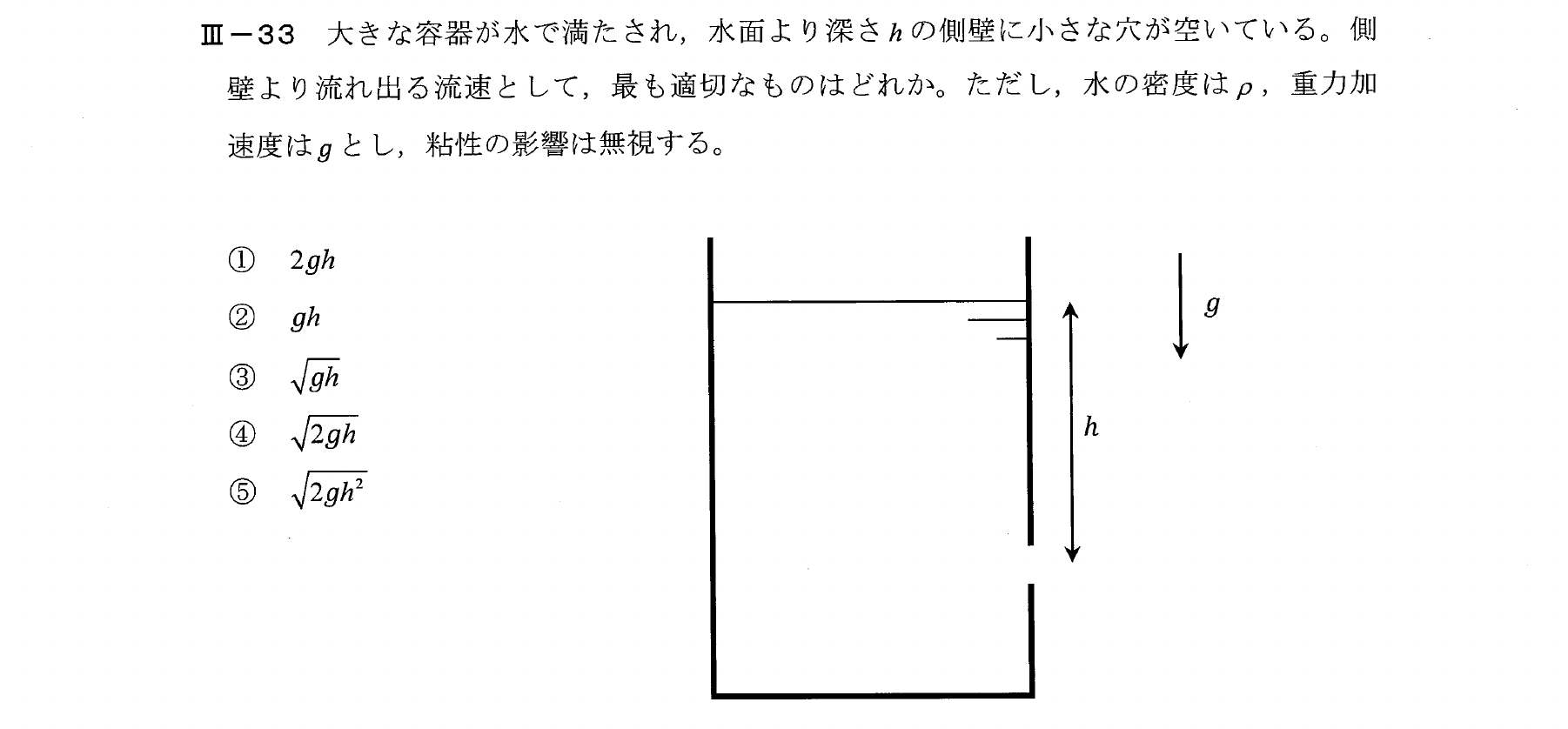
壁から流れ出る流速を\(u\)として、ベルヌーイの定理を立式する。
$$\rho g h=\frac{1}{2}\rho u^2$$
$$u=\sqrt{2gh}$$
【解答:④】
Ⅲー34

Ⅲー35


