【機械部門】技術士：R1（再）

特性方程式は次式となる。

$$ s^2+3s+2 = (s+1)(s+2) = 0 $$

$$ s = -1, -2 $$

システムの安定性の条件は、すべての極の実部が負であることである。

今回求まった極 \(-1\) と \(-2\)はいずれも負の実数である。

したがって、この系は安定である。

【解答：①】

覚える。

【解答：④】

関数\(F(s)\)を逆ラプラス変換するために、部分分数分解を行う。

$$F(s) = \frac{1}{s} – \frac{1}{s+1}$$

したがって、原関数\(f(t)\)は、

$$f(t) = u(t) – e^{-t}$$

問題文の条件より、\(t>0\)においては \(u(t)=1\)であるため、

$$f(t) = 1 – e^{-t}$$

【解答：③】

制御量：制御対象に属し、目標値に一致させるべき量。肢１

操作量：制御の目的を達成するために、制御対象に加える入力。肢２

偏差：基準量（目標値）と制御量との差。肢３

定常値：制御系が安定した後の出力値。肢４

基準量：目標として外部から与えられる値。肢５

【解答：②】

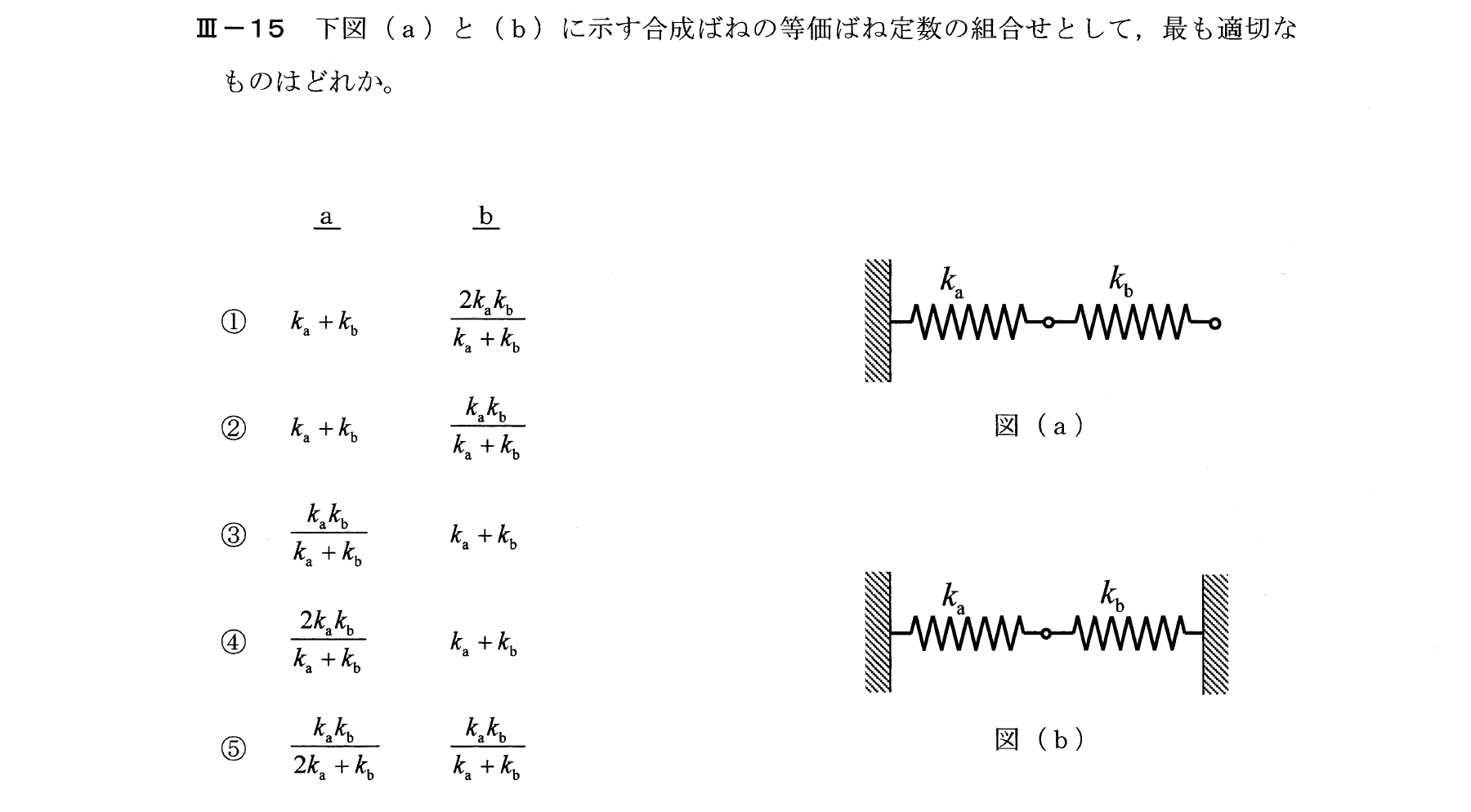
直列型と並列型（サンドイッチ型）の合成ばね定数である。

【解答：③】

（a）の固有角振動数 \(\omega_{n}\)は次式となる。

$$\omega_{n}=\sqrt{{\frac{k}{m}}}$$

（b）の固有角振動数 \(\omega_{n}\)は次式となる。

$$\omega_{n}=\sqrt{{\frac{ka^2}{\frac{1}{3}ml^2}}}$$

これらが等しくなるので、\(a\) について式を整理する。

【解答：④】

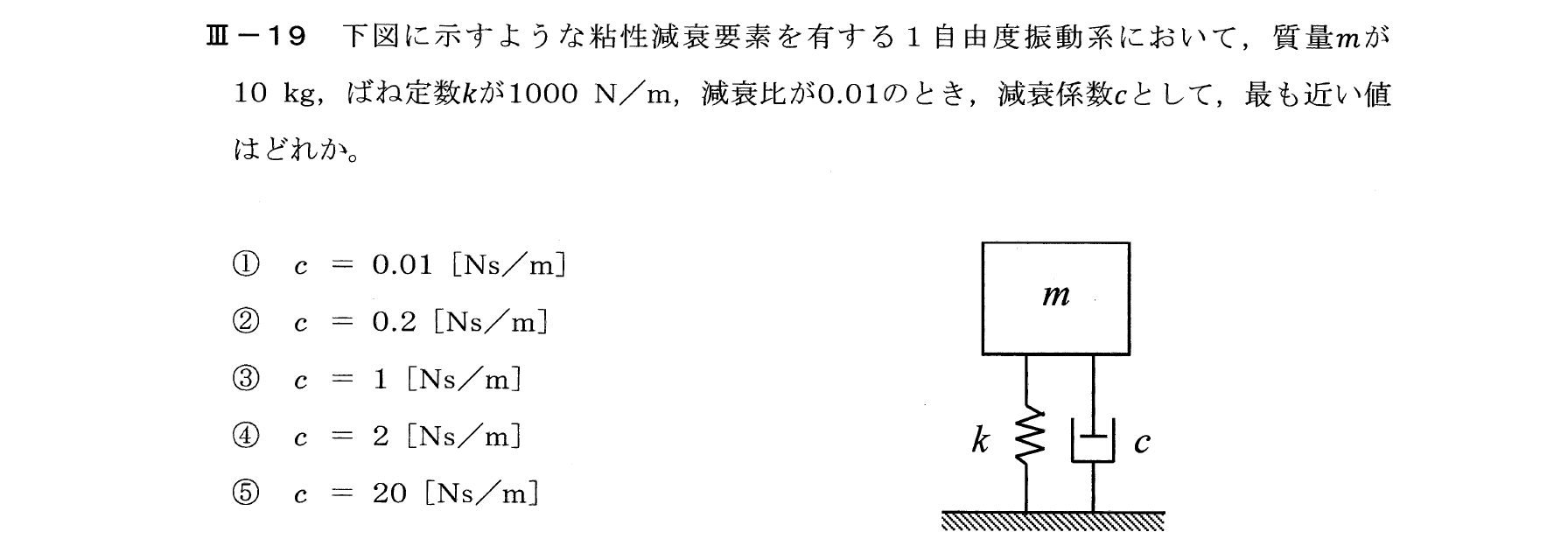
減衰比 \(\zeta\) は次式で表せる。

$$\zeta=\frac{c}{2\sqrt{mk}}$$

よって、\(c\) について式を整理して \(\zeta\) と \(m\) と \(k\) の値を代入する。

【解答：④】

覚える。

【解答：③】

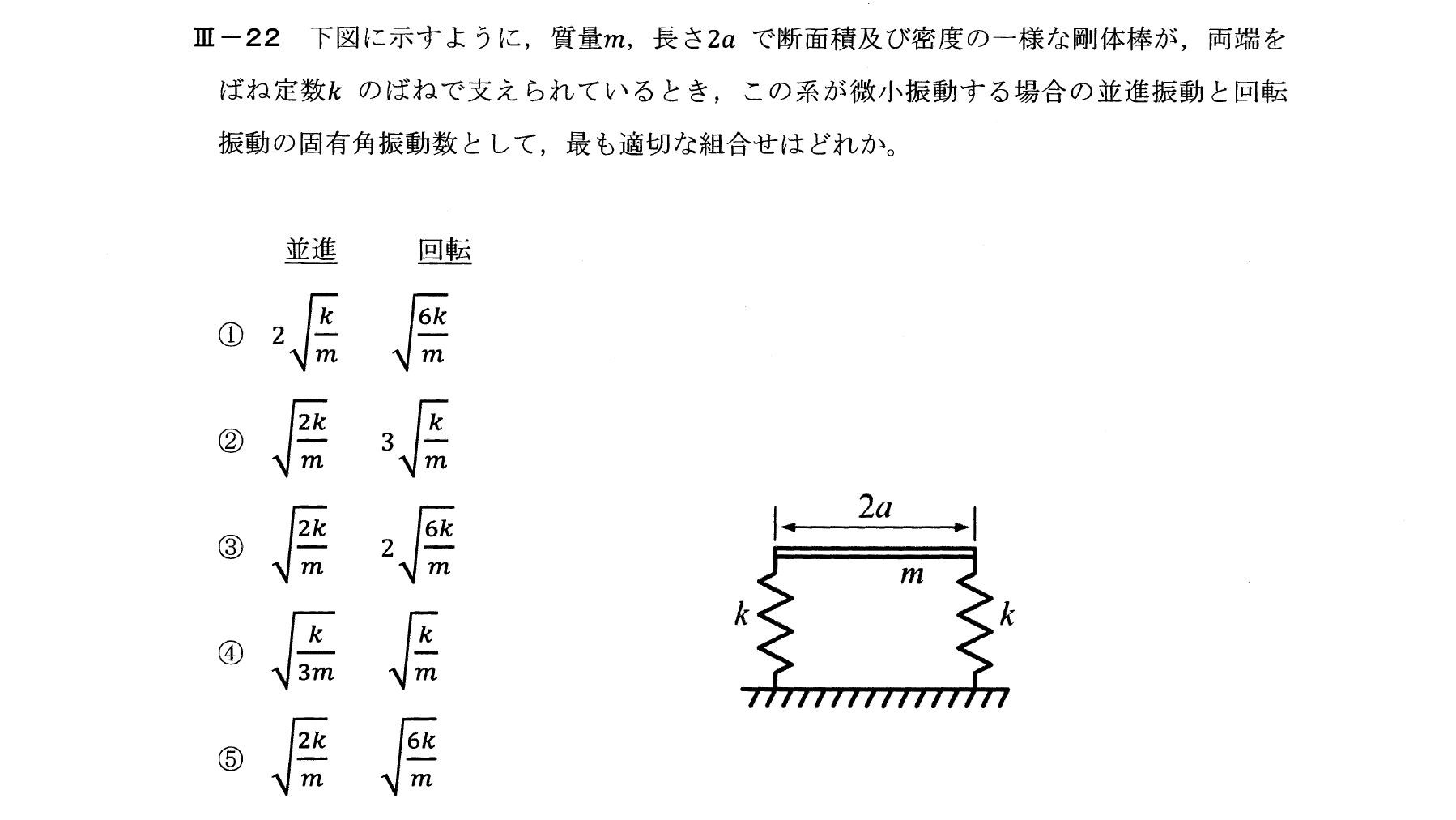
運動方程式は次式となる。

$$m\ddot{x}+2kx=0$$

よって、並進運動の固有角振動数 \(\omega_{n}\)は次式となる。

$$\omega_{n}=\sqrt{{\frac{2k}{m}}}$$

角運動方程式は次式となる。

$$I\ddot{\theta}+2ka^2\theta=0$$

ここで、 \(I\) は重心周りの慣性モーメントで、一様棒の場合は次式となる。

$$I=\frac{m(2a)^2}{12}$$

よって、回転運動の固有角振動数 \(\omega_{n}\)は次式となる。

$$\omega_{n}=\sqrt{{\frac{2ka^2}{\frac{1}{3}ma^2}}}=\sqrt{{\frac{6k}{m}}}$$

【解答：⑤】