Ⅲー1
Ⅲー2
Ⅲー3
Ⅲー4
Ⅲー5
Ⅲー6
Ⅲー7
Ⅲー8
Ⅲー9
Ⅲー10
Ⅲー11

Ⅲー12
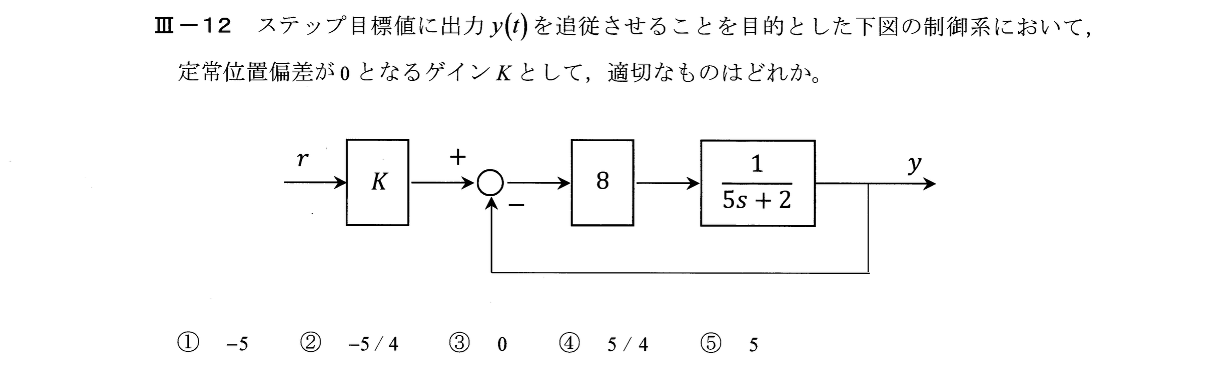
Ⅲー13
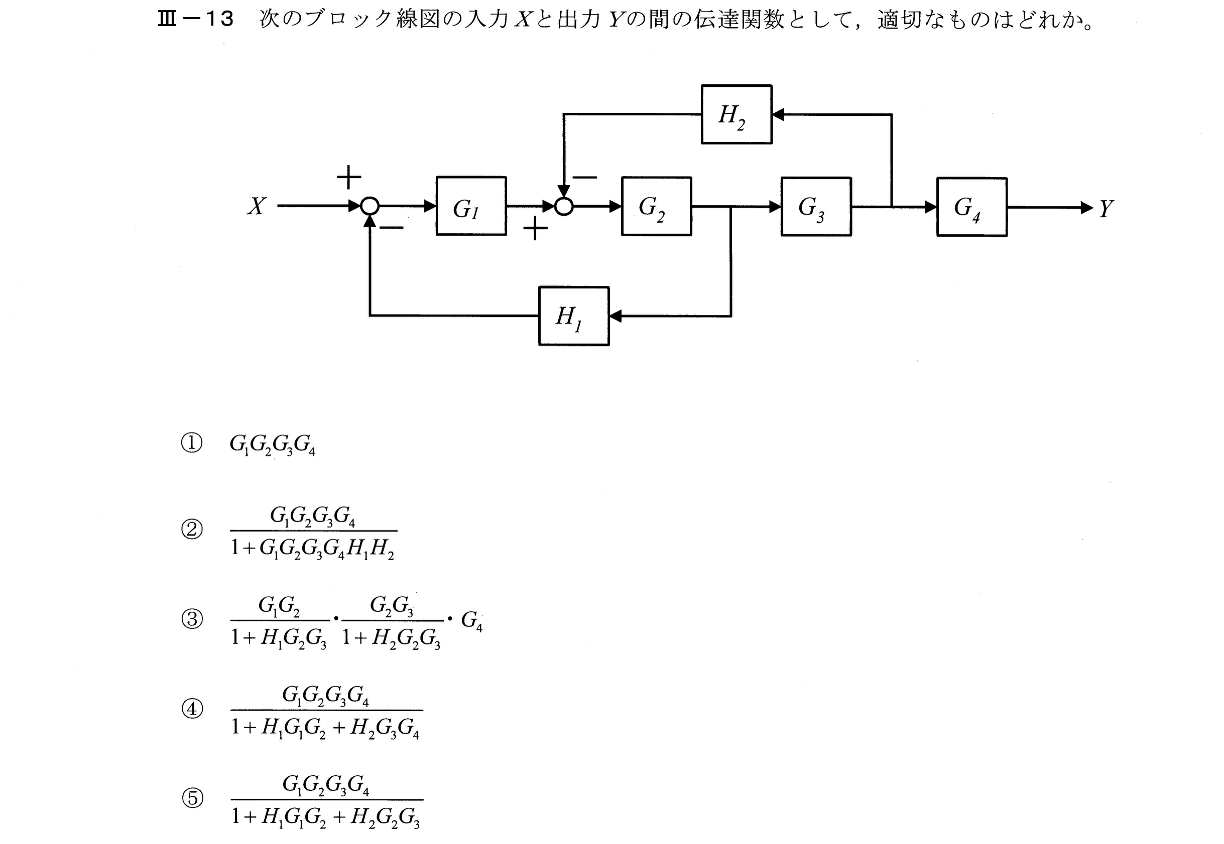
Ⅲー14

Ⅲー15
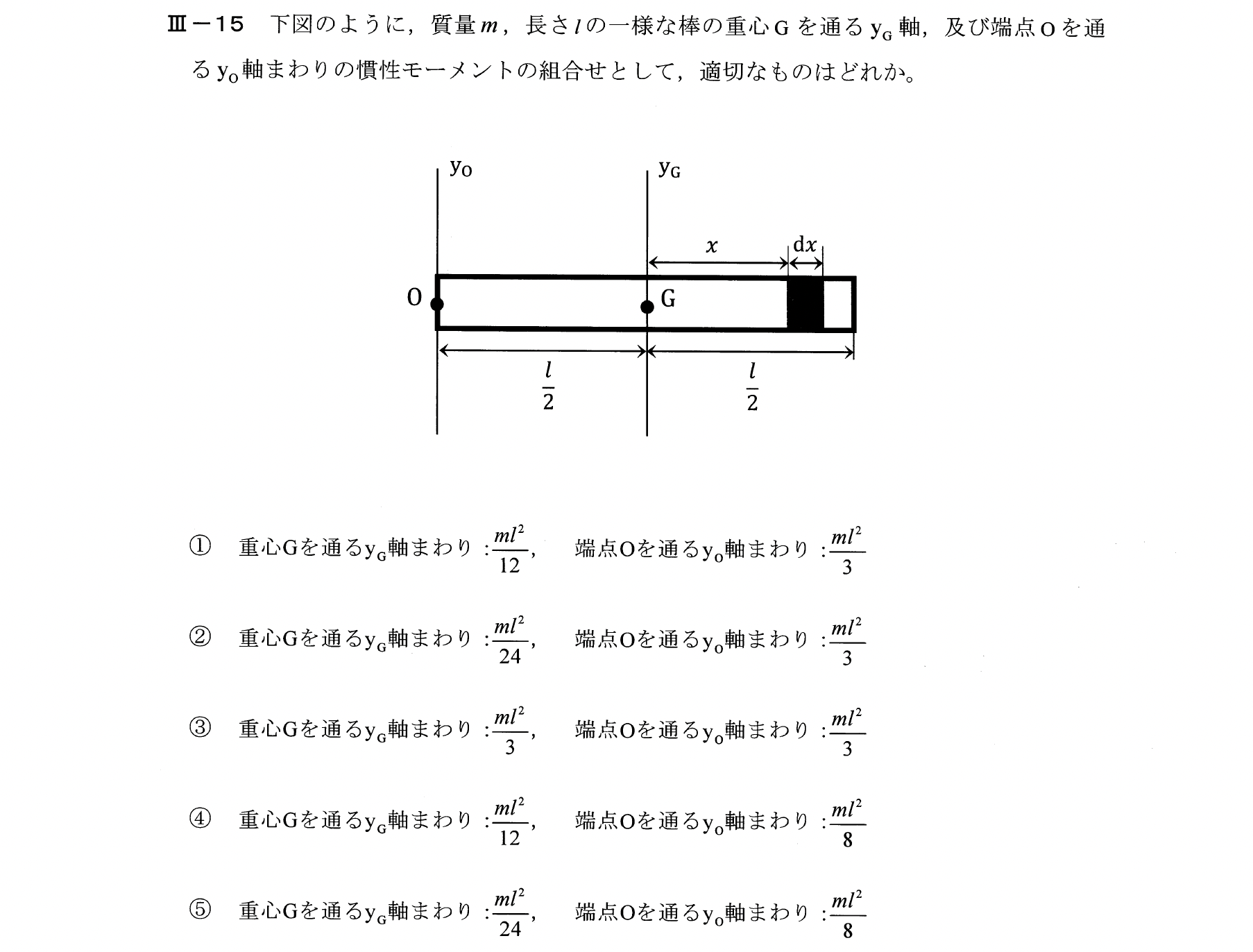
一様棒の場合、重心周りの慣性モーメント\(I_G\)は次式である。
$$I_G = \frac{ml^2}{12}$$
点O周りの慣性モーメント\(I\)は平行軸の定理を用いると次式となる。
$$I=I_G+\left(\frac{l}{2}\right)^2 m = \frac{ml^2}{12} + \frac{ml^2}{4} = \frac{ml^2}{3}$$
【解答:①】
Ⅲー16
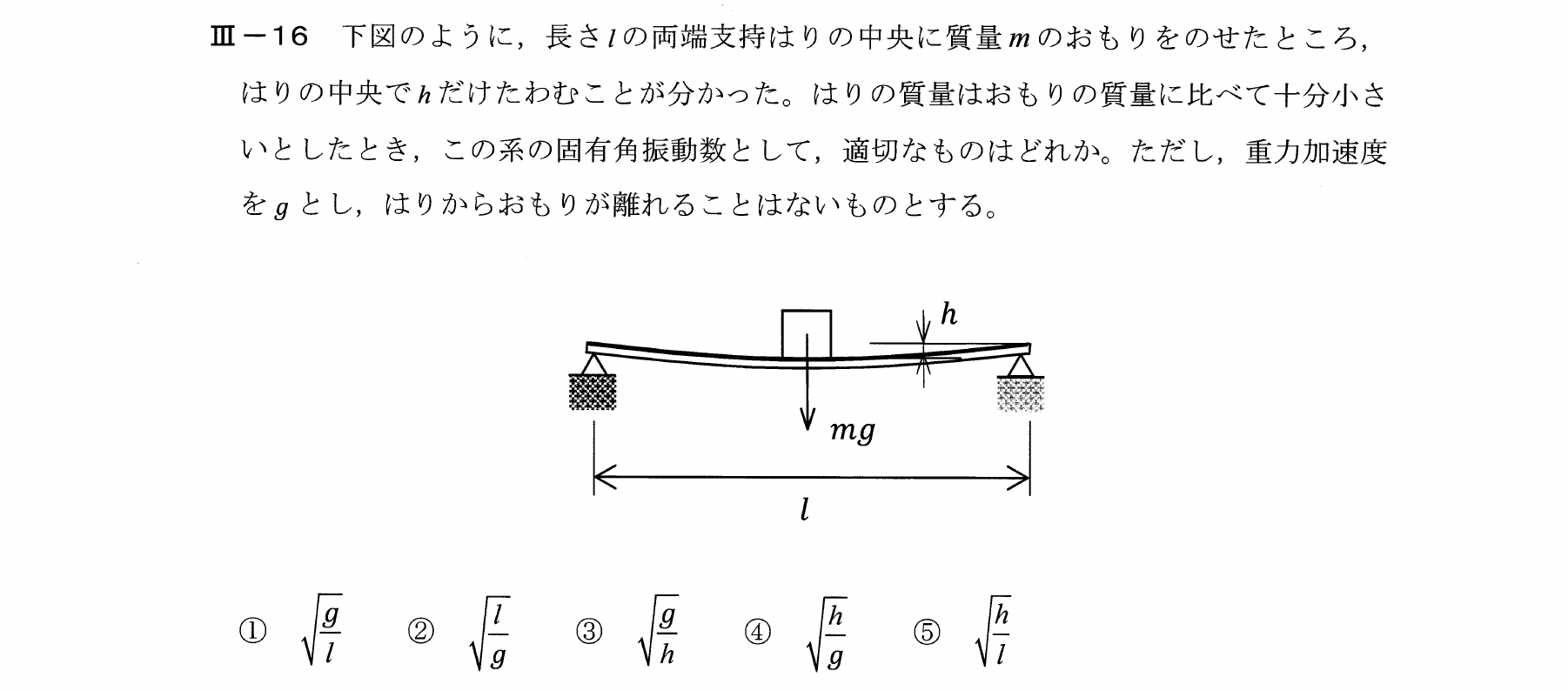
ばね定数を\(K\)とすると、力のつり合い式は次式となる。
$$Kh = mg$$
$$K = \frac{mg}{h}$$
よって、固有角振動数 \(\omega_{n}\)は次式となる。
$$\omega_{n}=\sqrt{\frac{K}{m}}=\sqrt{\frac{g}{h}}$$
【解答:③】
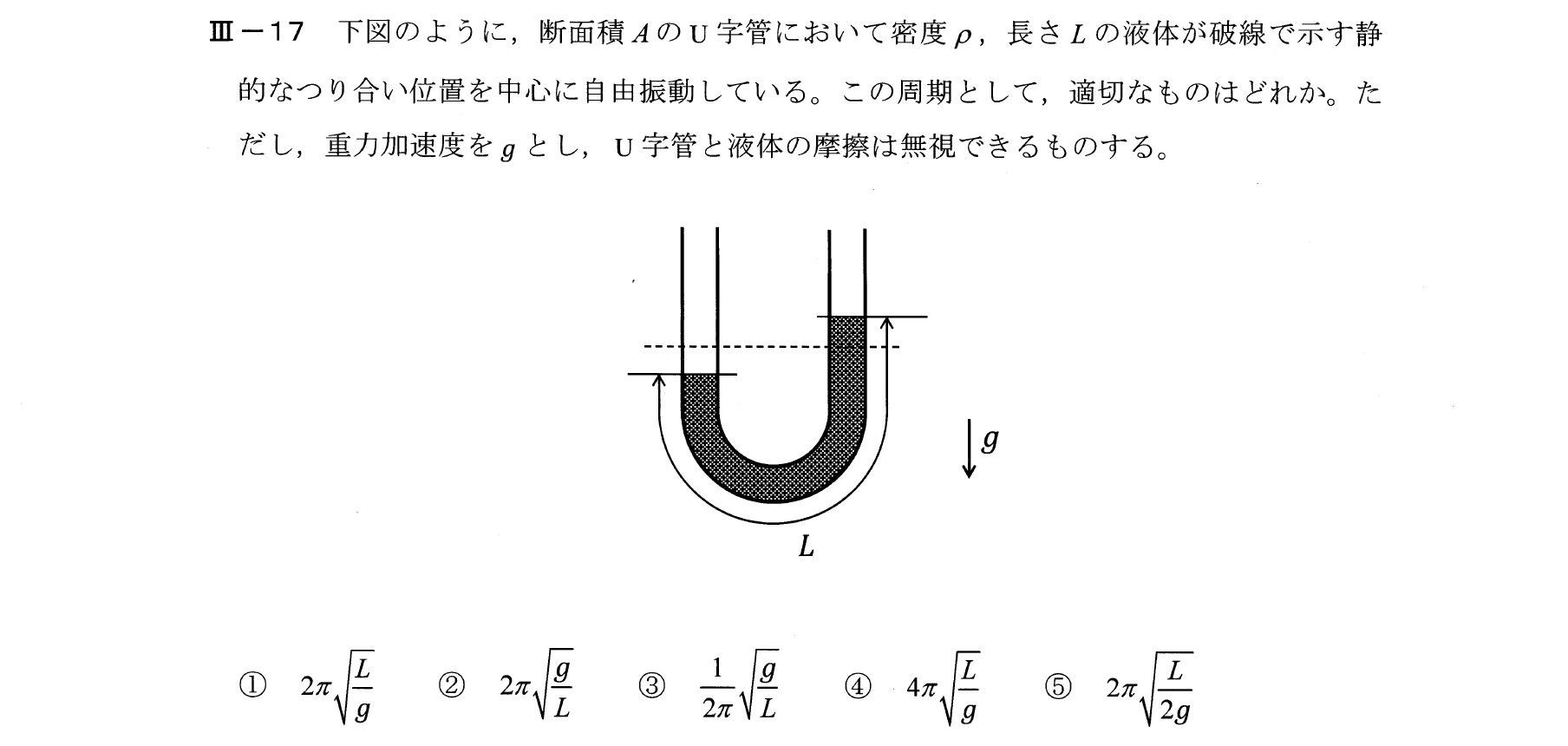
Ⅲー17
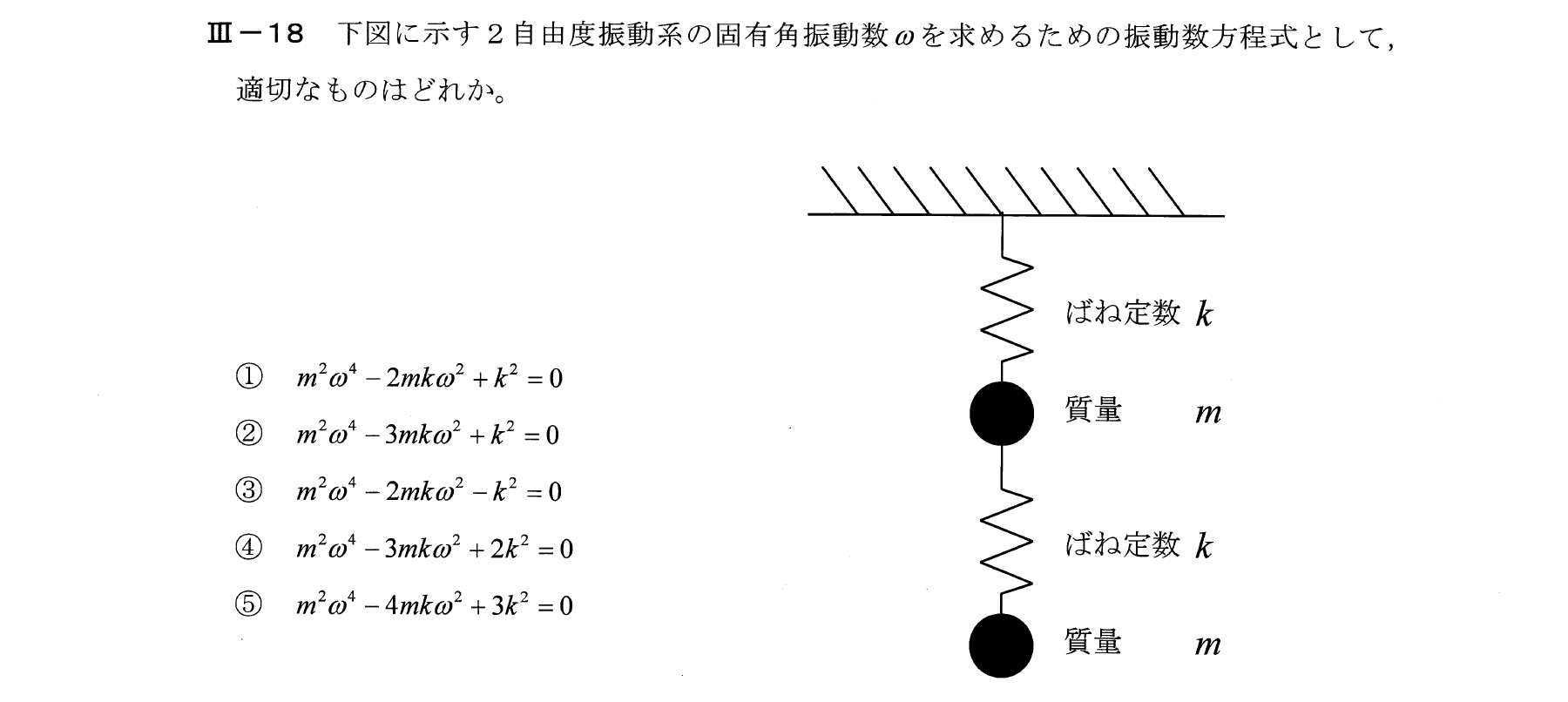
Ⅲー18
Ⅲー19
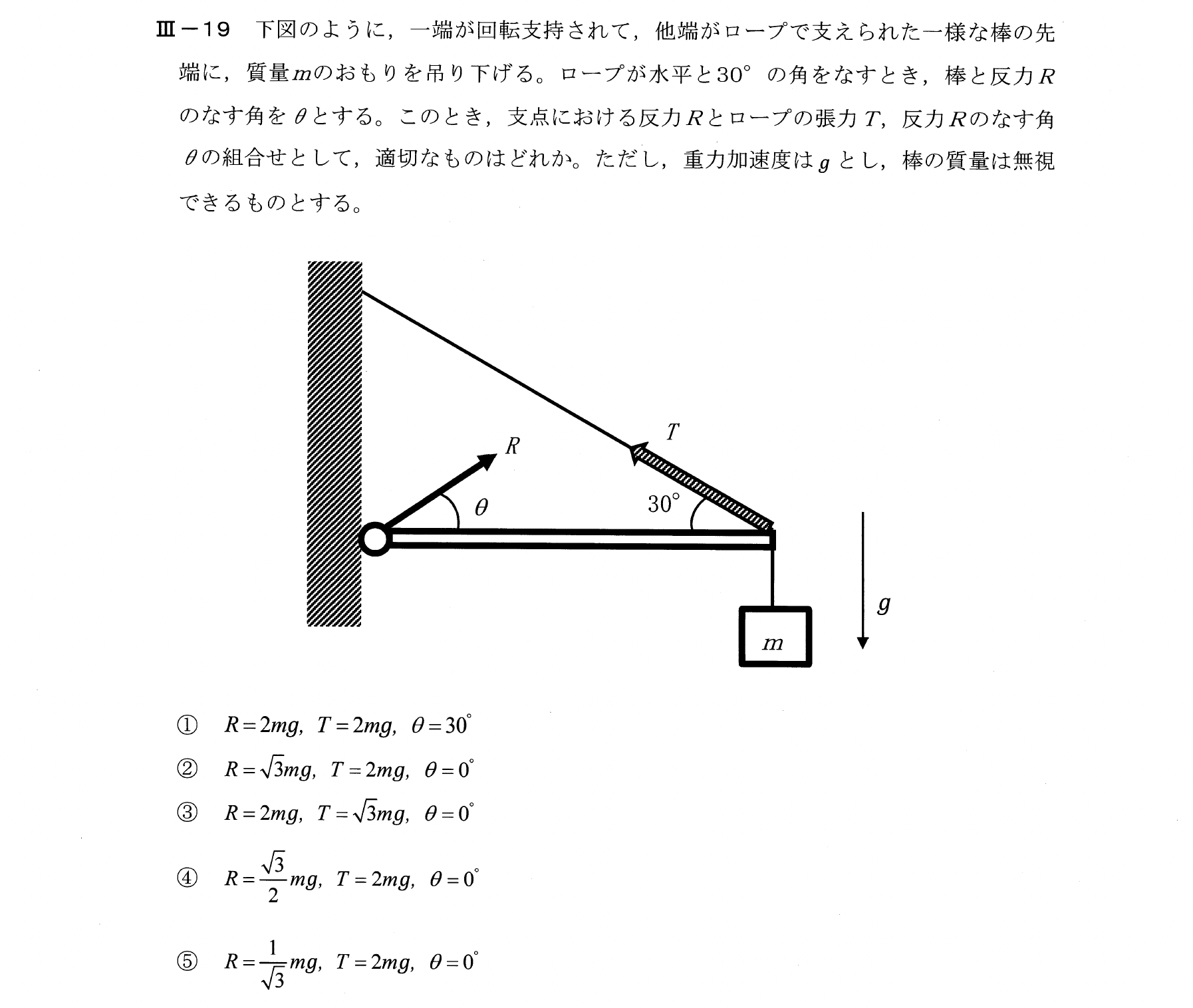
力のモーメントがつり合うためには、力の作用線が1点で交わる必要があるので、
\(\theta=0\)で力のつり合いを考える。
$$T\sin{30^\circ}=mg$$
よって、
$$T=2mg$$
したがって、
$$R=T\cos{30^\circ}=\sqrt{3}mg$$
【解答:②】
Ⅲー20

過減衰がある。
【解答:①】
Ⅲー21
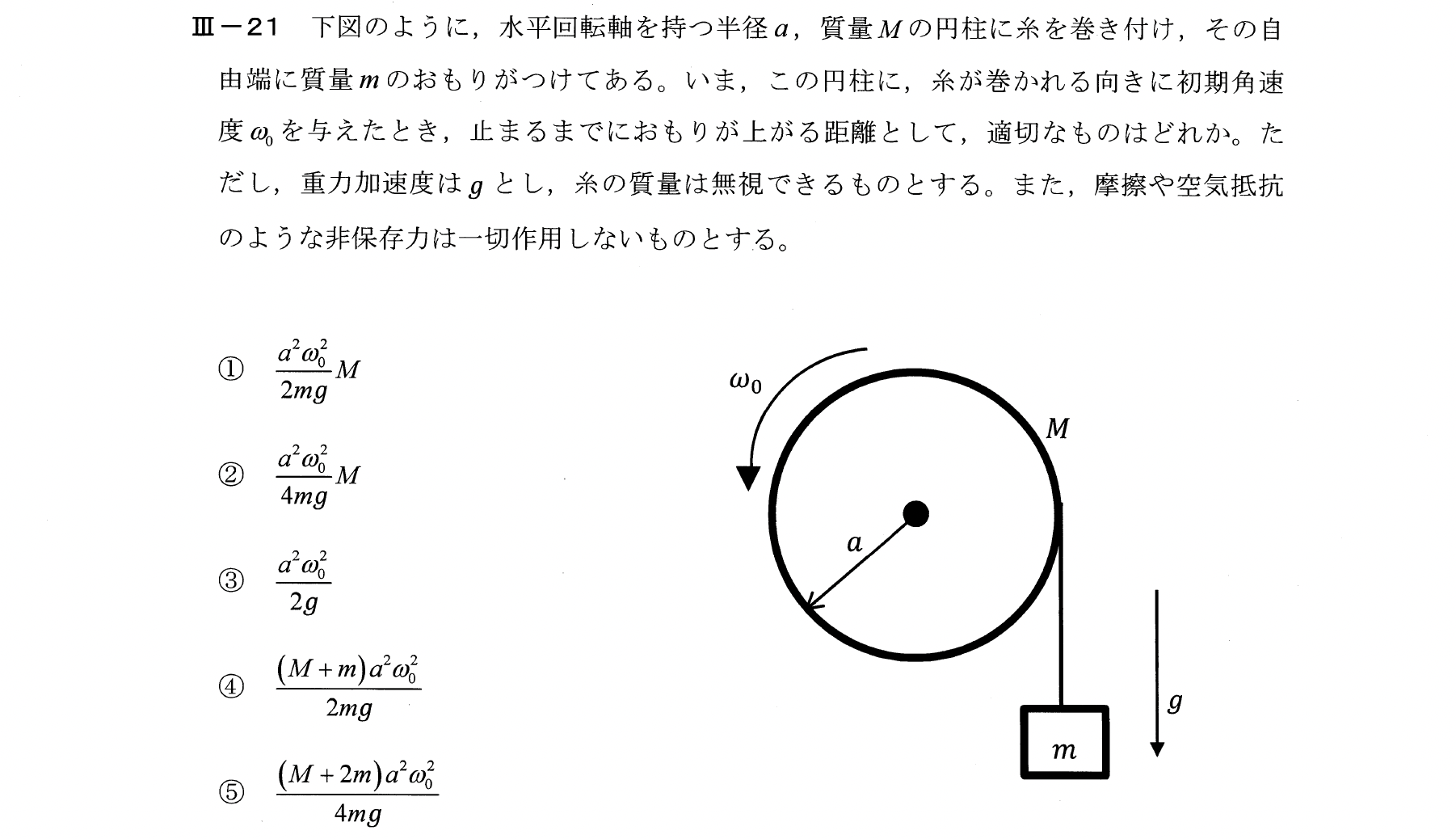
エネルギー保存則を立式する。
$$\frac{1}{2}I{\omega}^2 + \frac{1}{2}m{a\omega}^2= mgh$$
円板の場合、慣性モーメント\(I\)は次式となる。
$$I= \frac{Ma^2}{2}$$
これを代入して、\(h\)について式を整理する。
$$\frac{1}{2}\frac{Ma^2}{2}{\omega}^2 + \frac{1}{2}m{a\omega}^2= mgh$$
【解答:⑤】
Ⅲー22

覚える。
【解答:②】
Ⅲー23

比エンタルピー変化は次式となる。
$$\Delta h=C_p\Delta T$$
【解答:④】
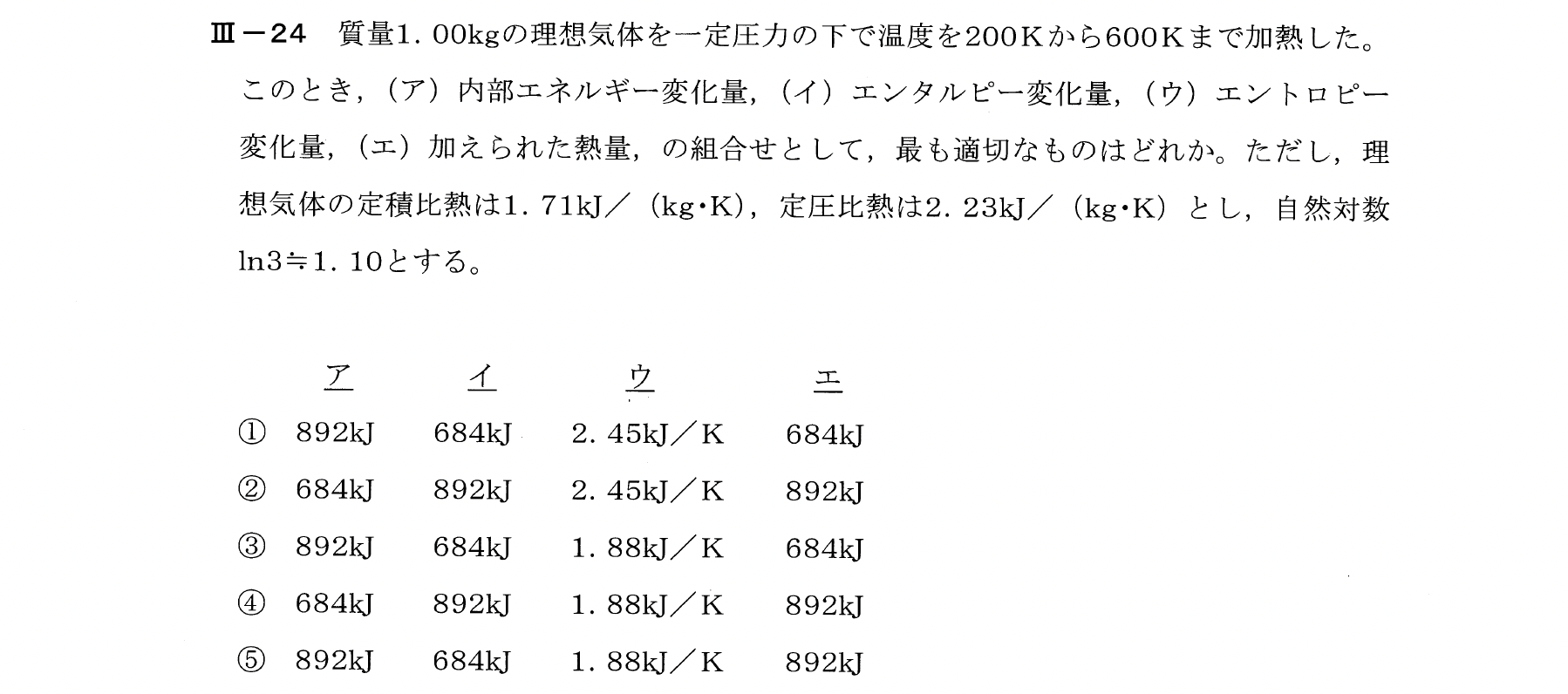
Ⅲー24
Ⅲー25

Ⅲー26

覚える。
【解答:②】
Ⅲー27

Ⅲー28

Ⅲー29

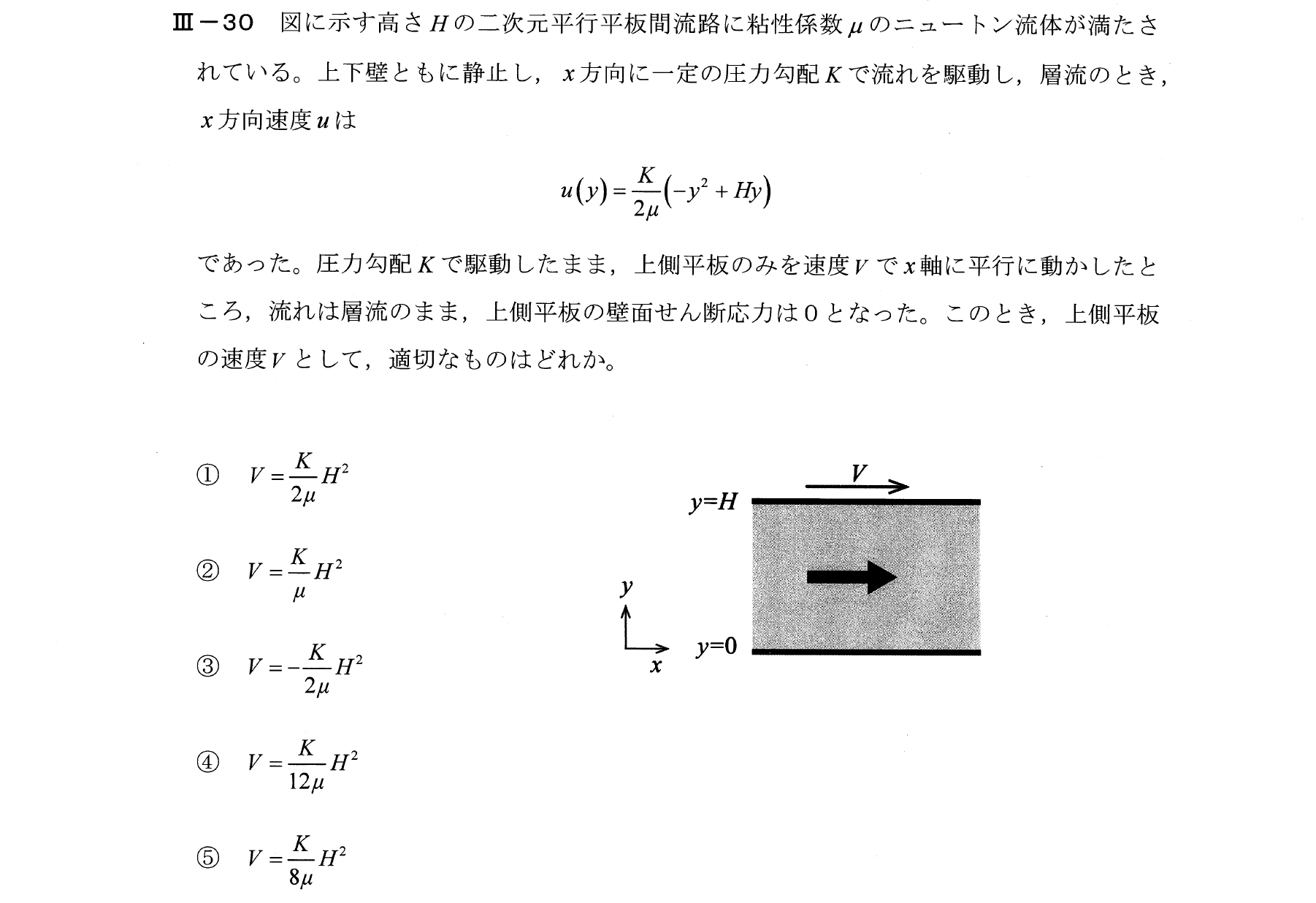
Ⅲー30
Ⅲー31

Ⅲー32
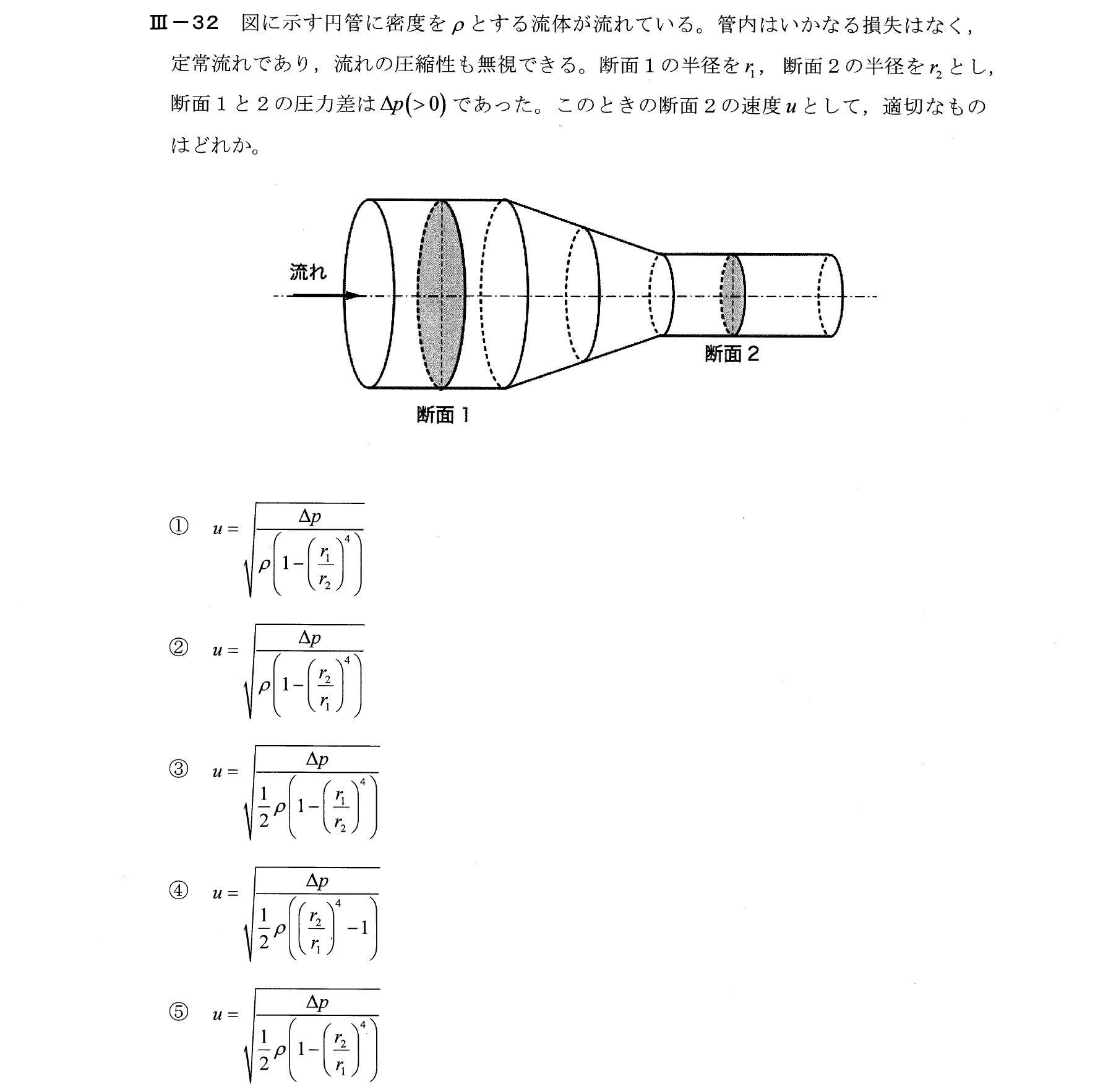
連続の式とベルヌーイの式を連立する。断面1における速度を\(u_1\)とする。
$$u_1\pi {r_1}^2=u\pi {r_2}^2$$
$$\frac{1}{2}\rho {u_1}^2=\frac{1}{2}\rho u^2 +\Delta p$$
【解答:④】
Ⅲー33

連続の式を立式する。
$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=(2x+y)+\frac{\partial v}{\partial y}=0$$
$$\frac{\partial v}{\partial y}=-2x-y$$
\(y\)について積分する。
$$v=-2xy-\frac{1}{2}y^2+C$$
【解答:④】
Ⅲー34

【解答:①】
Ⅲー35

ベルヌーイの式を立式する。
$$\rho g h=\frac{1}{2}\rho V^2$$
$$h=\frac{V^2}{2g}$$
【解答:④】

